Bonds Yields and their Relationship to a Bonds Price.
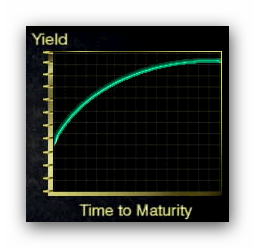
Understanding the pricing and yields of interest bearing instruments is critical to understanding bonds and the bond markets.
The relationship between a bonds price and its yield is really quite intuitive. Suppose a $1000 bond pays interest every six months at a rate of 8%. Suppose also that the yield currently being offered for similar bonds maturing at the same time is 9%. Would anyone be willing to pay $1000 for this bond? No not at all.
Most people would want some compensation for the fact that the coupons pays only 8%. At $1000 the bond isn't a good deal because you could invest in a new bond at 9%. If someone paid more than the face value of the bond this would be an awful deal. You’d be paying more than face value for the bond and also earning less than you could get by putting your money in a bond that was just being issued.

If a bond’s coupon pays less than the going rate, a bonds price will be less than face value, that is, “at a discount”, to increase its overall yield. And if a bond’s coupon pays more than the going rate, the bond will be priced at more than face value, that is, “at a premium”, to reduce its effective yield. In short, by simply raising or lowering a bond’s price, we raise or lower its effective yield.
Based on what we’ve discovered, how would we describe the relationship between price and yield? Is it direct or inverse?
Actually, price and yield always move in opposite directions. If we decrease a bond’s price, we increase its yield.
The rules for interest rates are also inverse. If interest rates rise then bond prices will fall. If interest rates fall then bond prices will rise. So if we saw the newspaper headlines below we would expect that the price of bonds would decline.
The Time Value of Money
To understand how the actual price of a bond is calculated, one must first understand that the value of a given quantity of money depends on when one will receive it.
Suppose interest rates are 8% and that interest is paid at the end of each year. We would say that the interest in this case is “compounded annually” because the interest is actually received and can be reinvested at the end of each year.
At 8%, an investment of $100 will grow to $108 in one year and to almost $117 in two years.
Financial people would say that at 8% interest rates, an investment with a “present value” of $100 has a “future value” at two years of $117. They might also say that a cash flow of $117 payable in two years is worth $100 dollars today.
Present Value Formula
PV = FV(1+i)-n or FV = PV(1+i)n
Where:
PV = present value
FV = future value
i = interest rate for compounding period (decimal equivalent)
n = number of compounding periods
How can we determine the future value of $155 at the end of three years if the interest rate is 9% and interest is compounded semi-annually (twice a year)?
PV=155 i = 0,045 n = 6 FV = ?
FV = PV(1+i)n = 155 (1 + 0.045)6 = 201.85
We can calculate present and future values very simply using the above formula. Try your hand at the above problem. Notice that the interest rate you must enter is the rate for the compounding period of six months, not the annual rate. An easier way to look at this is:
155(1+0.045)6 = FV
155(1.045)6 = FV
155(1.3022) = FV
155x1.3022 = 201.85
Future value is a result of the compounding of interest earned on the present value, or starting amount. As time progresses, the periodic interest is added to the starting amount and the next periodic interest amount is calculated based on that.
As such, the amount of interest earned over the entire time period can be found by subtracting the present value from the future value:
= 201.85 - 155 = 46.85 is the interest earned.
Bond Cash Flows
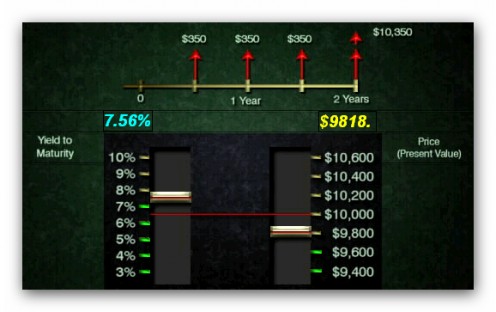
When one purchases a bond, one is really purchasing a specific series of future payments or “cash flows”. Take this bond, for example. It has a 7% semi-annual coupon and matures in exactly two years. The purchaser of this bond is really purchasing four coupon payments of $350 that will be paid once every six months, and a principal payment of $10,000 that will be paid when the bond matures.
The “price” of this bond is simply the present value of these cash flows calculated at the current interest rate or “yield to maturity” for bonds of this type. In our example, the desired yield to maturity for this bond is evidently 8%. We have therefore calculated the present value of each flow using 8%, then added them up to get the price $9,818.
By the way, notice that the price is lower than the face value of the bond. Because the bond’s coupon rate is less than the desired 8% yield, this is exactly what we would expect.
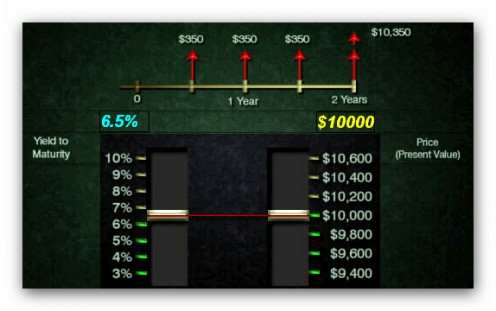
Let’s take this same bond and see what happens to the price as we change the desired yield. We can see that when the price equals the face value the yield is 6.5%.
The Price of a Bond
A bonds price can be expressed mathematically by the formula below. Notice that the formula is simply a series of present value formulas, one for each cash flow. Notice also that the compounding period is the same as the coupon period. If a bond pays a coupon every six months, that coupon interest can be reinvested every six months. The bond is in effect compounding semi-annually.

Now let’s use the formula to calculate the price of this bond. Look at the table which shows the amount and present value of each of the bond’s remaining four payments. We then total the values to find the price.

Recent events regarding the European financial crisis, particularly Greece's soveriegn debt is particularly interesting.
In March 2010 Greece issued 5 billion euro in a 10 year bond with a coupon of 6.50% which was around 300 basis points aboove the yield for 2 year german bunds. The issue was oversubscribed nearly two times at 14 billion euro and because of this the yield dropped to 6.02%. Still very high but lower than 6.50%. Considering what we have said in this hub where would you expect the price of the 10 year bond to be, below euro 10000 or above euro 10000? If you expected it to be above 10,000 you would be right. In fact the bond price was euro 10,081. Since that successful issue the markets became very nervous and existing Greek 2 year bonds at one point had a yield of 40%. This kind of yield effectively shuts the market down as who would want to sell at such high yields. Only the European central bank's intervention in the market lowered the yield on the Greek 2 year bonds.
In my next hub I will explain how a bonds price is calculated under various criteria.






