A Demystifying Mathematics Series Topic: Why "Imaginary" Numbers are Important to Everyone
We Do Need a Little Background. No, Stop! Read On!
If you already think you have been trapped into thinking that this is just another bate and switch tactic to get you to learn Math, (which you KNOW you ALREADY HATE!) just follow along. For the readers who either LOVE Mathematics or are curious about the theory involved I will include the technical jargon an formulas. Otherwise all of the examples will be shown with their solution.
The way which we need to proceed is some mathematical problems which even the great mathematicians had no solution for. So we will show some simple math problems as examples and tell a little history of how imaginary numbers got their unfortunate name. Then, we get to why imaginary numbers are really a part of everyday life and that they are not really imaginary at all. By the time you finish reading this article you will not only say "But that's simple" but you'll also say "why did they call them imaginary, that was dumb PR".
Some Simple Mathematics Explained
Let's look at a simple mathematical formula:
x + 3 = 5
Now in this case, the x is just a placeholder for a number. Think of the equation as being a question: "What number if added to 3 results in sum being 5?"
The answer to that is x must be 2. Besides that 2 is the ONLY possibility for x to be:
2 + 3 = 5
Mathematicians would say " we have solved for x". Equations of this sort, which are known as linear equations, or polynomial equations of the first degree. Also, if we make up other equations similar to this we always arrive at a single answer, as in x + 9 = 10, the one and only possibility for x to be in this case is 1.
There Are Other Equations to Consider.......
There are other equations which can have more than one solution. Let's take for example,
x2 - 6x + 5 = 0
the term x2 is said to be "x squared" which merely means x multiplied by itself ( i.e. "x times x"). This equation is known as a quadratic equation, where the word quadratic comes from the Latin word for square. It is also known as a polynomial equation of the second degree, because of the little number 2 in x2. As for the x itself, it could be written as x1 except by convention (read "time and effort saving", or laziness) the 1 is always omitted, kind of taken for granted. That is why in our previous example, x + 3 = 5, we said it was also referred to a an "....equation of the first degree".
Let's continue on with the solution in the next section.
Solving for "X" in the Quadratic Equation
Now we want to solve our equation:
x2 - 6x + 5 = 0
Since the reader was promised the solution to this (and all of the problems), there are two answers for x.
Consider the first x = 1. If x is one x times x is still 1. Now, we want to subtract 6 times 1 which equals 6 from the x 2 which was 1. Therefore we have 1-6+5 which equals 0.
O.K., thus far. Now consider if x was 5. Then the term x 2 becomes "5 times 5" or 25, minus "6 times 5, or 30, plus 5 : 25-30+5 surely equals 0.
So now we have two solutions to the equation and in general any polynomial equation of the second degree has a two solutions.

Mathematicians Couldn't Be Satisifed
The had to start looking at higher exponents of x. That is x3 which means "x cubed" or "x times x times x". Sure enough, equations of this form had three solutions.
In the case of x4 there were four solutions and x5there were five solutions............
Well, finally in 1796 Karl Friedreich Gauss proved that for any in the polynomial equation of degree n, for any integer n, there were exactly n solutions.
Carl Friedrich Gauß
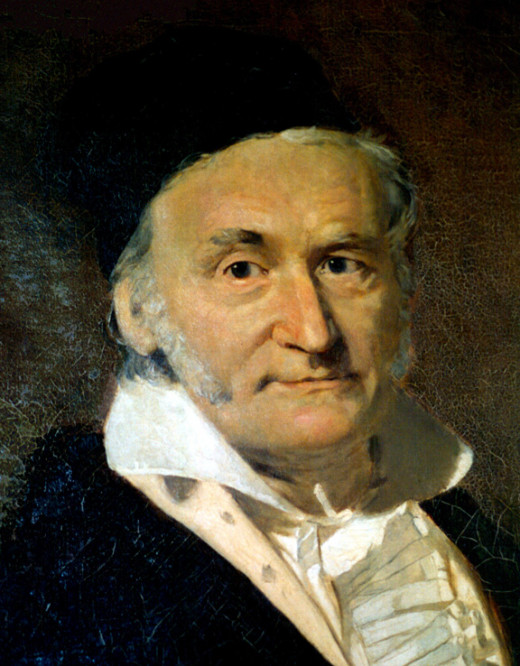
The Proof Held EXCEPT For One Case
We will skip over some of the subtleties of Carl Friedrich Gauß's work, although they are important they are not germane to the our current story. A serious problem arose in this nice general theorem, there was one case for which it did not work. The one case was:
x2+ 1 = 0
Well wait a minute, is seems to be a simple thing, -1 + 1 would equal 0. Yes,but this would mean that x2= -1, or that x was the square root of -1. From what rules applied in mathematics this was an impossibility.
A Mathematician Provides a Simple Solution
In 1777, the Swiss mathematician suggested that if x2= -1, or that x was the square root of -1 then let's just call the solution for the value for x in this case the letter i . Which is how imaginary numbers got their start.
Leonhard Euler Introduced "Imaginary" Number

Calculations with Imaginary Numbers
It is not just good enough for Euler to say, "Well, there's a problem here and I'll just fix it by setting the value for the square root of -1 to i and be done with it." A whole theory and set of rules about manipulating imaginary numbers ensued.
For example, if one has the number i one should be able to multiply it by a constant, so there is 2i , 3i , 4i, etc., we also know i2 is equal to 1. A whole new branch of mathematics was created called complex number theory.

But....But....What Is All This Math Good For?
Mathematicians up until the time of Euler were working with problems which consisted of a "real" component. This notion of what is"real" in terms of mathematics had to deal with counting. If you had two sheep (a male and a female) and a lamb came along, well then you had three sheep. The idea of zero sheep would later have a profound inmact on mathematics.
With the arrival of bank accounts, a new concept of "real" arrived, the overdraft or negative numbers.
Then there were factions, irrational numbers, etc.
Now with the imaginary number i defined, mathematicians now look at "real" numbers as just a special class of "complex" numbers, that is a "real" number with an imaginary part. Consider the number
18 as really being 18 + 0i , that is 18 really has a "shadow" component.
Our next snapshot and what follows will explain why the "imaginary" part of a complex number has become so important.
Windsock Computations Involve Imaginary Numbers

There Is A Lot More to the Theory
Admittedly, we have just scratched the surface of calculations involving complex number, but consider a real life example involving calculations with the windsock pictured above. I a pilot traveling at some speed in some direction down a runway not only need to know the speed of the wind he might be facing but he also needs to know direction. Is a headwind, tailwind, cross current. and how is it related to his direction and his speed. One example, speed can be considered the "real" component and direction modeled by the "imaginary" component.
In fact, many practical applications exist where two dimensional variables are involved and both dimensions are physically significant, from out airsock example to that of sizing photographs or moving a computer mouse.
Hopefully, Some of the Mystery of "Imaginary" Numbers Has Vanished
There are a great many books outside of the hardcore ones related to complex number theory and applications for university level pursuits. Two eary reads for the layman include:
Mazur, Barry (2003). Imagining Numbers (particularly the square root of fifteen. New York: Ferrar Strauss Giroux. ISBN 0-312-42187-7.
Nahin, Paul J. (2007).An Imaginary Tale . Princeton, NJ: Princeton University Press ISBN 0-691-02795-1

![An Imaginary Tale: The Story of [the square root of minus one]](https://m.media-amazon.com/images/I/51165kgitzL._SL160_.jpg)