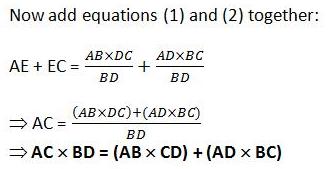Claudius Ptolemy
Claudius Ptolemy’s dates are given tentatively as 85 to 165 AD, but we do not know exactly when he was born or died. We do know that he made astronomical observations at Alexandria between 127 and 151 AD, and for that reason he is also often referred to as Ptolemy of Alexandria.
Ptolemy was an astronomer of some note. As a prerequisite to his work on astronomy and the accurate measurements he needed to make, Ptolemy studied trigonometry, and his greatest work was a thirteen book treatise on trigonometry named the Mathematical Syntaxis . This work is more frequently known by the Arabic name Almagest which means ‘the greater’. This name comes about from a comparison with a similar but inferior work written by Aristarchus and others which was referred to as ‘the lesser’.
Ptolemy’s Almagest contains very accurate trigonometric tables. Central to the compilation of these tables was the theorem that has become known as Ptolemy’s Theorem (see below).
Ptolemy also made a contribution to the way we measure angles. The division of the circumference of a circle into 360 equal parts seems to have been in use since the time of Hipparchus around 430 BC, and this idea translated into dividing a complete turn into 360°. However, it was Ptolemy who subdivided the degree into sixty equal parts, named ‘minutes’, and the minute into sixty equal parts named ‘seconds’.
Ptolemy’s calculations also led him to an approximation for pi which he gave as 3.1416 in modern notation.
A contribution of Ptolemy to mathematics
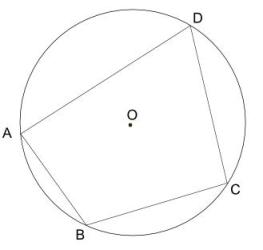
A cyclic quadrilateral is a quadrilateral drawn with all four of its vertices on the circumference of a circle.
Ptolemy gave the following theorem named Ptolemy’s Theorem:
If ABCD is a cyclic quadrilateral, then the product of the lengths of the diagonals is equal to the sum of the products of pairs of opposite sides.
i.e. AC × BD = (AB × CD) + (AD × BC)
The proof of this theorem uses similar triangles.
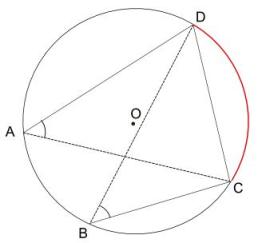
It also requires knowledge of another well-known theorem variously called The Angles subtended by the same arc theorem or The Angles in the same segment theorem which states that:
If CD is an arc of a circle and A and B are any other two points on the circumference of the circle on the same side of chord CD, then Angle DAC = Angle DBC
Proof of Ptolemy’s Theorem
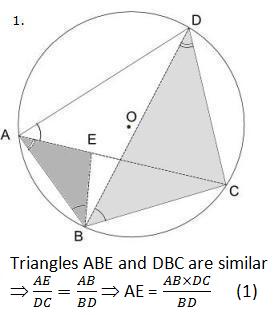
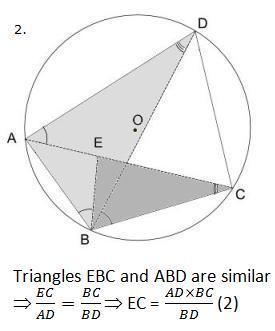
Draw in the diagonals AC and BD and find the point E on AC such that Angle ABE = Angle DBC
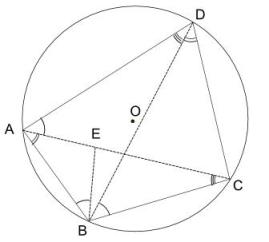
Equal angles are shown on the above diagram as follows:
Angle ABE =Angle DBC = Angle DAC (one arc)
Angle BAC = Angle BDC (two arcs)
Angle ACB = Angle ADB (three arcs)
Now consider two pairs of similar triangles: