Quadratic Simultaneous Equations. How to solve a pair of linear and quadratic equations by substitution.
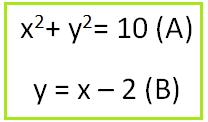
There are many ways of solving a pair of equations when one is linear and the other is quadratic. But the easiest way is to substitute the linear equation into the quadratic equation. Before you attempt the example below, make sure you can solve a pair of linear equations using the substitution method. You can use these 5 steps below to help you solve a pair of quadratic and linear equations:
1) Make x or y the subject of the linear equation. If there is a 1x then make the x value the subject or if there is a 1y make y the subject – this will make the algebra easier to handle in later steps.
2) Next substitute your linear equation into the quadratic equation. Make sure you put a bracket around the algebra that you substituted into the equation. You should now have an equation just in terms of x or just in terms of y.
3) Next expand the brackets and simplify the equation so that is in the form ax2 + bx + c = 0
4) Factorise the equation and solve to find the value or values of x. If the equation cannot be factorised then apply the quadratic formula.
5) Finally substitute your x values back into the linear equation to work out the corresponding y values.
Let’s look at an example of solving simultaneous equations where one is linear and the other is quadratic.
Example 1
Solve this pair of simultaneous equations:
x2+ y2= 10 (A)
y = x – 2 (B)
1) Make x or y the subject of the linear equation. If there is a 1x then make the x value the subject or if there is a 1y make y the subject – this will make the algebra easier to handle in later steps.
y is already the subject of the linear equation so you need to put this into equation A.
2) Next substitute your linear equation into the quadratic equation. Make sure you put a bracket around the algebra that you substituted into the equation. You should now have an equation just in terms of x or just in terms of y.
Next put this linear equation into the quadratic equation.
x2 + (x-2)2 = 10
3) Next expand the brackets and simplify the equation so that is in the form ax2 + bx + c = 0
x2 + (x-2)(x-2) = 10
x2 + x2 -2x -2x + 4 = 10
2x2 -4x + 4 = 10
2x2 – 4x -6 = 0
Divide this equation by 2 as all the terms are multiples of 2:
x2 – 2x -3 = 0
4) Factorise the equation and solve to find the value or values of x. If the equation cannot be factorised then apply the quadratic formula.
(x+1)(x-3) = 0
So either x + 1 = 0 or x -3 = 0
Which gives x = -1 or x = 3
5) Finally substitute your x values back into the linear equation to work out the corresponding y values.
Start with x = -1 and substitute this into y = x – 2
y = -1 -2
y = -3
And when x = 3
y = 3 – 2
y = 1
So the solutions to this quadratic simultaneous equation are (-1,-3) and (3,1)