How to Solve 4 simultaneous equations with a 4 by 5 matrix
CHRISTIAN HEADS UP!
1. For those of you who believe in God, jump to the last paragraph at the end of this hub to see what was said about God.
4 UNKNOWN CHEMICAL ELEMENTS
2. Let us suppose you are given a problem, whether at work or school, in which you have 4 molecules( possibly constituents of a macro-molecule), and the information you have on them is the number of atoms of each element in each molecule, and each molecule has 4 elements in common. Your job--should you decide to accept it, and I recommend that you do if you do not want to be fired or flunk the course--is to determine which elements that God structured within each molecule.
SETTING UP THE EQUATIONS
3. In algebra variables are assigned letters as X,Y,Z, but when you go above 3 then it is convenient to write them as X1, X2, X3 and X4. The numbers should be subscripts, but it is too much of a pain to use the toolbar subscript feature. These represent our unknown elements right off the periodic table. The first molecule has 5 atoms of X1, 5 of X2, 5 of X3, and none of X4. When you use the rules and definitions of chemistry these 15 atoms add up to a molar mass of 135( rounded to the nearest integer as they all are). So we will condense this to equation form: 5X1 + 5X2 + 5X3 + 0X4 = 135. This molecule and the other 3 molecules are listed at L1, which means location one. You do not know what the elements are so perhaps the number, 135, was found by experimentation.
MATRICES CONDENSE AND ORGANIZE INFORMATION
4. Matrices, as used in math, is a way to condense and organize the information even more than the equations by assigning a column space to each of the variables, X1, X2, X3 and X4, and then just don't write them down because it is understood where they are. This is done at L2. Also if an element is negative then a negative sign goes in front of it but if it is positive then nothing goes in front--just another way to get rid of the clutter.
ELIMINATION METHOD
5. We essentially use the elimination method to solve this matrix and sites as those I have linked for us below will give us a good idea on how the mathematical process of elimination works.
Ways of solving system of equations
- An Algebra Homework Involving Simultaneous Equations in 3 Unknowns
Pemekwulu shows us how to solve simultaneous equations by 3 different ways. One way was equating the equations. - Simultaneous equations
dkhchua, shows 4 ways to solving a system of equations: elimination, substitution, matrix and graphical. He also has a practical application. - Solving Simultaneous Equations in 10th Grade
article 3 uses the elimination method, and defines terms. - Solving simultaneous equations by the elimination me...
catman 3000 uses the elimination method, and has links for more help.

REMEMBER THE BALANCE: DO ON THE RIGHT WHAT WAS DONE ON THE LEFT
6. A foundational concept used in the elimination process is something we learned in basic algebra: An equation is like a balance on which we do on the right of the equals sign what we did on the left, so that the equation remains balanced. This is one of the justifications for the row manipulations at L5 and L6, etc.
SOME TERMS USED IN LINEAR ALGEBRA
7. At L2 we have a 4 by 5 matrix( 4 rows, 5 columns). The first 4 columns are called, in this case, the coefficient matrix. We will call the last column the molecular mass, or molecular weight, matrix. When the two are put together like this it is called an augmented matrix. The numbers inside the matrix are called elements( not to be confused with the chemical elements in this problem). The main diagonal, or just diagonal, of this matrix is represented by a1,1; a2,2; a3,3 and a4,4. If we do not know the value of our coefficients then they are typically assigned, ai,j where i represents the row location, and j the column location as at L3. L3 represents the echelon form of a matrix, and L4 is the reduced row echelon form. We eliminate the coefficients at L3 and L4, making them into zeros, by using legitimate mathematical techniques based upon theorems; therefore, elimination with eraser is frowned upon. They call this technique, "Pick up your final check on Friday." Geometrically speaking, a matrix can be thought of as a system of vectors. If the coefficient matrix is greater than 3X3 then the vectors are, or may be, vectors in hyperspace. For example, when you solve 2 variable linear equations geometrically, your solution is where the two lines intersect. In our case we have 4 lines intersecting at a point in hyperspace, and its coordinates are (12, 1, 14, 16), which we will be determining shortly.

CONVERTING A MATRIX TO ECHELON FORM
8. I think the work below is pretty self explanatory. The first line of L5 has, 4R3 -- 5R4---->R4 1st which means 4 times row 3 minus 5 times row 4 and the answer is to be put on row 4. The "1st" after that means to do it first, because if you don't keep the order straight you'll just get confused. At L5.1 is just doing some of the arithmetic that I can't do in my head . . . What? . . . . Well, you knew I wasn't Stephen Hawking when you started reading this hub. At L7 on the 1st line we have a minus one times row 3, and then 1/2 times row 4 and then switch them: put row 3 on row 4 and row 4 on row 3.

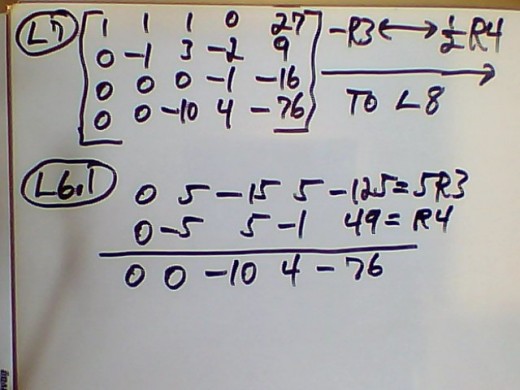
USE "BACK SUBSTITUTION"
9. L8 is in echelon form. We know that X4 is equal to 16 because if we put X4 back into the equation then we have 1X16 = 16; therefore, we use back substitution and plug that value into row 3 and calculate X3 from L11 to L13, and get a value of 14 atomic mass units. We then substitute X3 and X4 into row 2, which is the 2nd equation, at L14 to L18 and we get X2 = 1. We substitute X2, X3 and X4 into row 1 at L19 to L21 and get X1 = 12. These are the atomic mass units of these elements. We look them up on the periodic table to determine what they are: X1 is carbon, X2 is hydogen, X3 is nitrogen, and X4 is oxygen. After we do the reduced row echelon form, I will tell you the significance of these amazing molecules that God, by Jesus Christ, created with His understanding( Isaiah 29:16; 40:28; Psalm 104:24; 147:5).

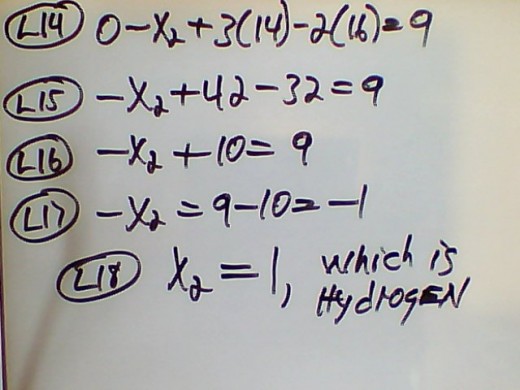
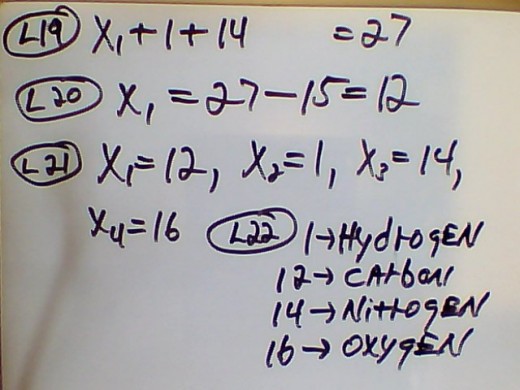
REDUCED ROW ECHELON FORM( rref)
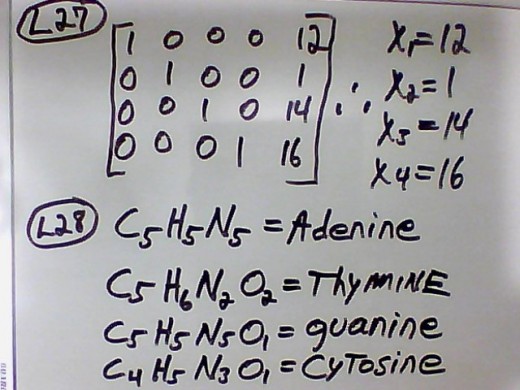
10. Ok, let's get this in reduced row echelon form( rref) so your boss doesn't say, "What's this? This is not in reduced form. What? You expect me to do the back substitution?" You are probably familiar enough with the work to understand what is being done; therefore, let's jump to L27. Notice here at L27 that in rref we can read the values right off the matrix. At L28 we interpret the information we calculated and determine that these are the constituent nucleotide pairs( adenine with thymine, and guanine with cytosine) that God structured into DNA molecules. We can go back to the original equations at L1 and rewrite them. So C5+H5+N5 = 135 is the first equation, which is interpreted as 12(5)+1(5)+14(5) = 135. We do the same thing for the other three equations.


DISCREPANCY ON "ECHELON" FORM
11. Echelon form is defined as: 1. "The leading entry of each row is to the right of the leading entry of the preceding row." 2. "All entries directly below the leading entry of each row are zeros." 3. All rows that consist entirely of zeros are below any rows that contain nonzero entries."
12. Some textbooks define echelon form with the further qualification that the leading entry is a 1. Since there is this discrepancy anyway then I prefer the definition that the leading entry can be any number. However, I have found no discrepancy concerning the definition of rref( reduced row echelon form); in this case all the diagonals are to be 1.
THE TI-89 CALCULATOR
13. I intend to write an entire hub on this calculator, but for now let me point something out to you: Everything we have done in this hub, the ti-89 calculator can do in . . . oh, I don't know . . . I would say about 2 seconds! There is a technological term for this accomplishment---WOW!
GOD---CREATOR OF DNA
14. It is amazing how God can put a few billion of these nucleotide pairs together, in a specific order, so that a DNA molecule becomes the reference library for other molecules and cells to use in order to build our physical bodies. As I said at
the informational density of DNA is enormous, and it is enormously impressive. But the unfathomable aspect of this sub-microscopic realm is how God, through Jesus Christ, made this informational reservoir so dynamic. From the time we are born we are constantly learning and we may continue to add to our knowledge from 18 years old to 30 with more schooling. We do this so we can learn how to design things, make things; repair, create and invent things. We learn how to heal ourselves and our beloved animals. Collectively we have ascended to remarkable levels of achievements with the brains that God has designed, created, and given to us. Yet these microscopic molecules and cells can read( miraculous in itself) the information stored within the geometric structure of DNA, and with no learning process, they are able to use the wisdom God gave them( Job 38:36) to take that information they have read and processed, and then make proteins more complex than any machine all of mankind has ever built. I intend to supplement the hub, "DNA--A Witness for God," with additional parts giving more details of this spectacular realm that is so demonstrative of God's omniscience.










