Larry's Symmetry Puzzle

As a child, how did you learn to distinguish between left and right.
Overview of handedness
At one point in my childhood, I got tired of confusing left and right. As a memory aid, I imagined myself in the back seat of the family car, looking forward. Then I remembered that the steering wheel was on the left hand side. After that, whenever I was the least bit confused, I would call up that mental picture.
Other children have used different mnemonics. An acquaintance remembered that there was a birthmark on her mother's right forearm. This kind of active learning on the part of children is quite creative, if I do say so myself.
Still other children learn the concept of left and right by osmosis, without struggling, and without the need for trickery of any kind.
The smarter breeds of dogs learn the distinction between left and right at an earlier age than humans do. That's why a year-old Border Collie is able to remember that he's supposed to be on the left side of the owner, when they go out for a walk, and the human gives the "Heel" command.
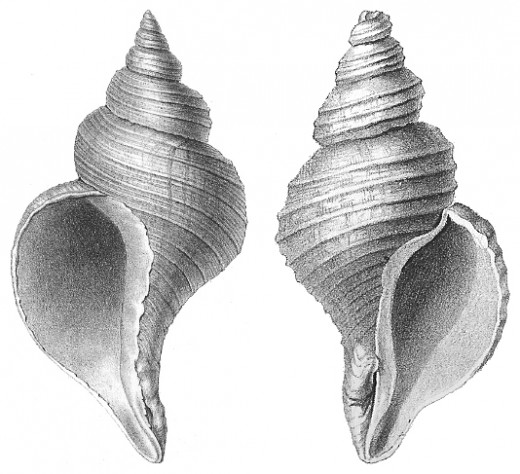
Mathematicians and chemists often use the word "chirality," instead of handedness. A three-dimensional object is said to be chiral (pronounced kiral) if it cannot be superimposed on its mirror image. The classical example is the human hand. Another example: each of the two sea snail shells in the top picture.
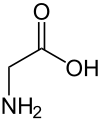
Glycine, as shown in the picture, is the only common dietary alpha amino acid that's non-chiral. In principle, you could take a molecular saw, and cut it in half.
The two halves would be mirror images of each other.
Likewise, the two halves of the human body are mirror images of each other, except when one is wearing a ring, for example.
Yes, I know that the human heart is somewhat off-center. But you don't see the heart--or any other internal organs--when you're looking at a person.
Anyway, the human body is said to have bilateral symmetry, because of the mirror image effect.
Speaking of mirrors, some ethologists (scientists who study animal behavior) use mirrors to gauge self-awareness in animals. In some species, the male will try to fight with his mirror image!
In other species, an animal will notice that that his reflection in the mirror duplicates every motion that he makes, and will intuitively understand that he is simply seeing himself in the mirror. There are undoubtedly other clues as well. For example, the mirror image does not have a scent, and does not make noise. Animals that have passed the Mirror Test include Bottlenose Dolphins, Elephants, European magpies, Great Apes, and Orcas.
The puzzle
Suppose that you have four steel ball bearings (spheres), and that you paint each of them a different color. After the paint dries, you glue three of them together to form a base. After the glue dries, you put the cherry-colored one on top.
You've just constructed a chiral object. And you did it with four objects, each of which has bilateral symmetry.
Here's the conundrum: What is the smallest number of bilaterally symmetric objects that you need to glue together in order to make a chiral object?
The geometric approaches in the next section are not the only ones that will yield the desired minimum.

Two solutions
Start with the Great Pyramid of Giza, which is shown in the photo. Restore the casing stones in order to make a smooth surface. Then paint the right face red, and the left face blue. After the paint dries, saw off the back half of the pyramid, which is hidden from view in the picture. You'll have two triangular pyramids--or tetrahedrons.
The back tetrahedron has bilateral symmetry, but the front one does not, because of the paint.
Then saw straight down along the edge that separates the colored faces. The front tetrahedron splits apart into two smaller tetrahedra, each of which has bilateral symmetry. Again, if you glue the two colored tetrahedrons back together, the result will not have bilateral symmetry.
By the way, be sure to get permission from the Egyptian government before doing any major renovations on the Great Pyramid. :)
Here's another solution with a different flavor: Using honey, 'glue' two side-by-side, wedge-shaped pieces of cake together. The two pieces have the same size and shape. One piece has chocolate frosting on top; the other has white frosting.
Copyright 2012 and 2013 by Larry Fields







