The Slope of A Line

SLOPE OF A LINE

The concept of slope of a line is one of the most important topics in Mathematics.

Its concept also plays important role in Physics.

Definition of a slope:

If (X1_, Y1) and (X2_, Y2) are any two points on a line, then the slope of a line is expressed by the following formula :

m = (Y2 - Y1) / (X2 - X1) where X2 not equal to X1

This shows that the slope of a line is the ratio of the difference of the ordinates of

any two points on the line to the difference of the abscissas. This means that (Y2 - Y1) and ( X2 - X1) are directed distances.

Slope of a horizontal and vertical line

If the two given points are on a horizontal line, it implies that they have the same ordinate , therefore the slope is zero since Y2 - Y1 = 0. If the two points are on a vertical line, it implies that they have the same abscissas, then (X2 - X1) equals zero and the slope of a vertical line is "undefined" since division by zero will give undefined quotient.

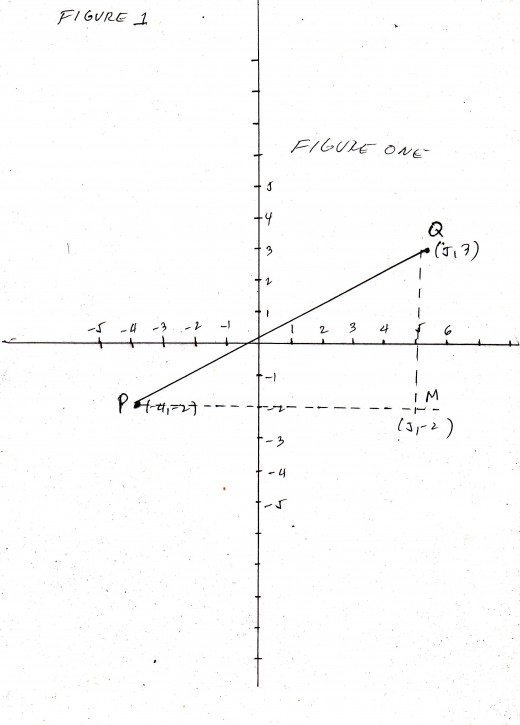
Example : Determine the slope of the line segment joining P( -4, -2) and Q(5, 3)

Solution:

Either point may be taken as (X1, Y1) and the other as (X2, Y2).

m = (Y2 - Y1 ) / ( X2 - X1)

m = ( 5 - ( - 4)) / (3 - (-2) ) = 5 + 4 / 3 + 2 = 9/5

In figure one, (see attached figure) as we move along the line from left to right ( from P to Q ), the ordinate increases 9 as the abscissa increases 5. In contrast, if we move from right to left, the ordinate decreases 9 as the abscissa decreases 5. In either case, the slope is 9/5.

In general the slope of PQ is the ratio of QM to PM and it is positive if one variable increases as the other increases or if the variable decreases as the other decreases. The slope of a segment is negative if one of the variables increases as the other decreases.

The slope of a line is also the measure of the steepness of a straight line. The greater the slope , the greater is the steepness of the line.

A positive value for a slope resembles a line graph that is leaning to the right. A negative value for a slope resembles a line graph that is leaning to the left.

Positive value for slope also indicates direct proportionality between two variables while negative value for slope indicates inverse proportionality between two variables.

Application of Slope : Variation

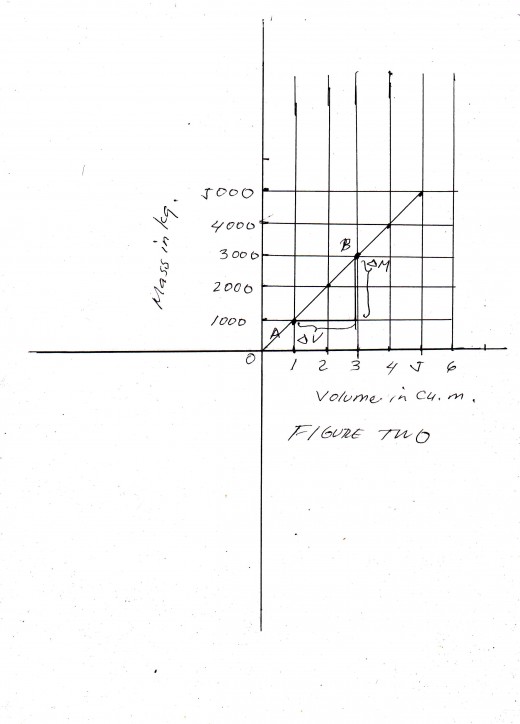
The direct proportionality between two quantities maybe clearly shown by means of a graph. Figure Two shows the graph of volume of water in cubic meters against mass in kilograms The direct proportionality between the volume and the mass is shown by the straight line.

Let us take two points on the graph, for instance points A and B. The difference in mass or the difference in the Y-coordinates , for the two points is ∆ M = 5,000kg - 1000kg.

The corresponding difference in volume is ∆ V = 3 cubic meters - 1 cu. m. = 2 cu. m

The symbol ∆ is read as "delta" means change in or difference in the value of. The ratio of ∆Y to ∆X , which is the ratio . change in mass to the change in volume is known as the "slope" of the straight line. The slope is also the constant ratio "k", of the mass to the corresponding volume. Hence this constant slope is also known as the density of water.

D = M / V

SOURCE :

COLLEGE ALGEBRA by

Adele Leonhardy