A Tangent And A Radius Make A 90 Degree Angle At The Point Of Contact (Circle Theorem Help)
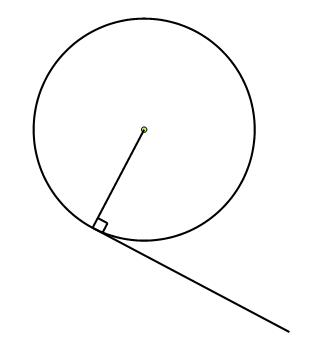
If you have a tangent meeting a radius then the angle that the tangent and the radius make is a right angle. In test questions look out for right angled triangles and kites when applying this circle theorem. It might also be useful to note that two tangents are equal in length made from the same point (this is usually quite obvious from the diagram).
A tangent is a line that touches edge of the circle and a radius is a line half way across the centre of the circle.
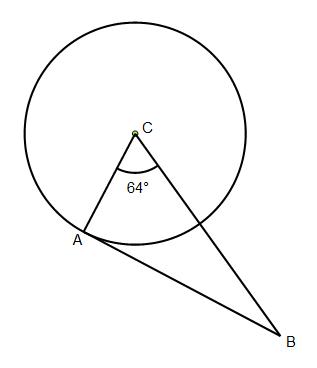
Example 1
Work out angle BAC and angle ABC. Give reasons for your answers.
Let’s begin by work out angle BAC.
Angle BAC can be found using the above circle theorem.
So angle BAC = 90 degrees (a tangent and radius make a right angle at the point of contact)
Angle ABC can now be found as you should know that angles in a triangle add up to 180. So subtract angle 64 and 90 from 180:
180 – 90 – 64 = 26 degrees.
So angle BAC is 26 degrees (angles in a triangle add up to 180).
Let’s take a look at a harder example using the circle theorem above.
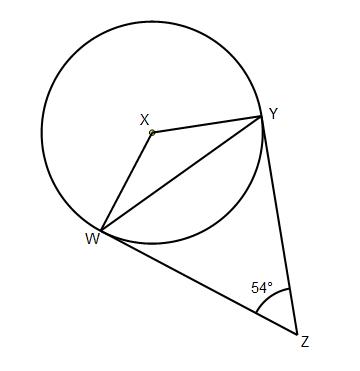
Example 2
In the diagram shown, find:
a) Angle WXY
b) Angle WYX
Answers
a) Angles XWZ and XYZ are both right angles as lines WZ and YZ are both tangents that are meeting the radius.
Now shape WXYZ is a quadrilateral so to find angle WXY you can use the fact that angles add up to 360 degrees in a quadrilateral:
360 – 90 – 90 – 54 = 126 degrees.
So angle WXY is 126.
If you are asked for reasons then quote, a tangent and a radius make a right angle, and angles in a quadrilateral add up to 360.
b) Triangle WXY is an isosceles triangle. So you can use the answer from part a) and the fact that angles in a triangle add up to 180:
180 – 126 = 54.
54/2 = 27 degrees
So angle WYZ = 27 degrees.
Summary
So just remember the fact that a tangent and radius make a right angle at the point of contact. It is normally quite obvious from the diagram, but students lose marks by not quoting this circle theorem if asked to give reasons for their answer! You might also need to quote the circle theorem that two tangents are equal in length if you are given two tangents.



