Area of a triangle = 0.5absinx - using the two side lengths and the angle between them.
The alternative method to calculating the area of a triangle (instead of 1/2bh) is by using the formula:
Area of triangle = ½absinx
a and b are the two side lengths of the triangle and x is the angle between the two sides.
This formula can be used in all types of triangles, but make sure you have 2 side lengths and the angle between them. This formula is useful when working out the area of the segment and in situations when the perpendicular height of the triangle is not given
Example 1
The diagram shows triangle ABC. AB is 7cm and AC is 12cm. Angle BAC is 21⁰. Work out the area of the triangle giving your answer to 1 decimal place.
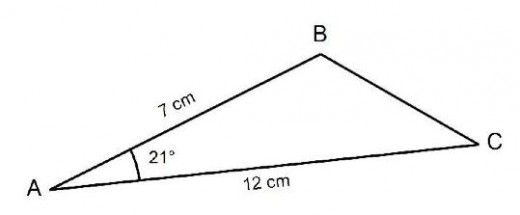
Here you are given two side lengths and the angle between these two sides so you can use the formula Area of triangle = ½absinx.
So a = 7cm and b = 12cm (It doesn’t matter if you do a=12 and b = 7) and angle x = 21. All you need to do now is substitute these numbers into the formula for the area of a triangle:
Area of triangle = ½absinx
Area of triangle = ½ × 7 × 12 × sin(21)
Area of triangle = 15.1 centimetres squared rounded to 1 decimal place.
So the formula gives an answer of 15.1 cm²
Example 2
The diagram shows triangle DEF. DE is 14 m, EF is 11 m and DF is 15.4 m. Angle DEF is 75⁰. Work out the area of the triangle giving your answer to 1 decimal place.
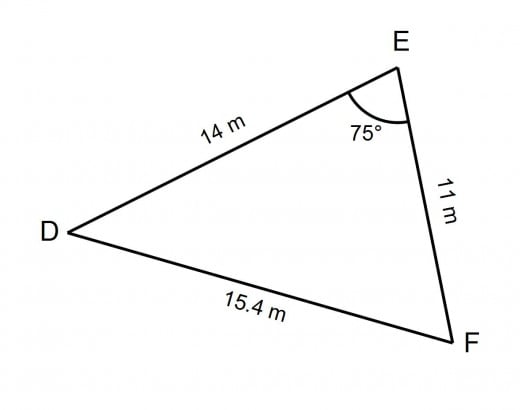
On this example you need to be careful which side lengths to use. Make sure you choose the side lengths either side of the given angle.
Therefore you have; a = 14 m and b = 11m (again it doesn’t matter which one is a and which one is b) and angle x = 75⁰. The other length of 15.4m is not needed to work out the area of the triangle - it is only there to catch you out. All you need to do now is substitute these numbers into the formula for the area of a triangle:
Area of triangle = ½absinx
Area of triangle = ½ × 14 × 11 × sin(75)
Area of triangle = 74.4 m² (rounded to 1 decimal place).
So the formula gives an answer of 74.4 cm² for the area of the triangle.
As you can see using the formula ½absinx for working out the area of a triangle is not as difficult as it looks as long as you have a scientific calculator. Just remember to use the two sides and the angle between.