Aryabhatta: The Indian Mathematician
Life and Works of Aryabhata
ARYABHATTA, or, as written by the Arabs, ARJABAHR, a celebrated Hindu mathematician, and the earliest known author on Algebra, is now generally believed to have lived about the beginning of our era. Nothing, however, has yet appeared that can give us the slightest information as to the place of his birth, or the time when he lived; nor is there, as far as we know, any tradition or record extent from which we can collect any of the circumstances of his life; even his period is still a matter of dispute. We must, therefore, content ourselves with whatever notices we find of Aryabhatta and his system in the various writers on astronomy and other mathematical sciences whose authority is established and cannot be called into doubt.
Aryabhatta is the first writer on astronomy to whom the Hindus do not allow the honour of a divine inspiration. Writers on mathematical science distinctly state that he was the earliest uninspired and a merely human writer on astronomy. This is a notice which sufficiently proves his being an historical character.

The chief doctrines which Aryabhatta (Aarya-Bhatt) professed were the following:
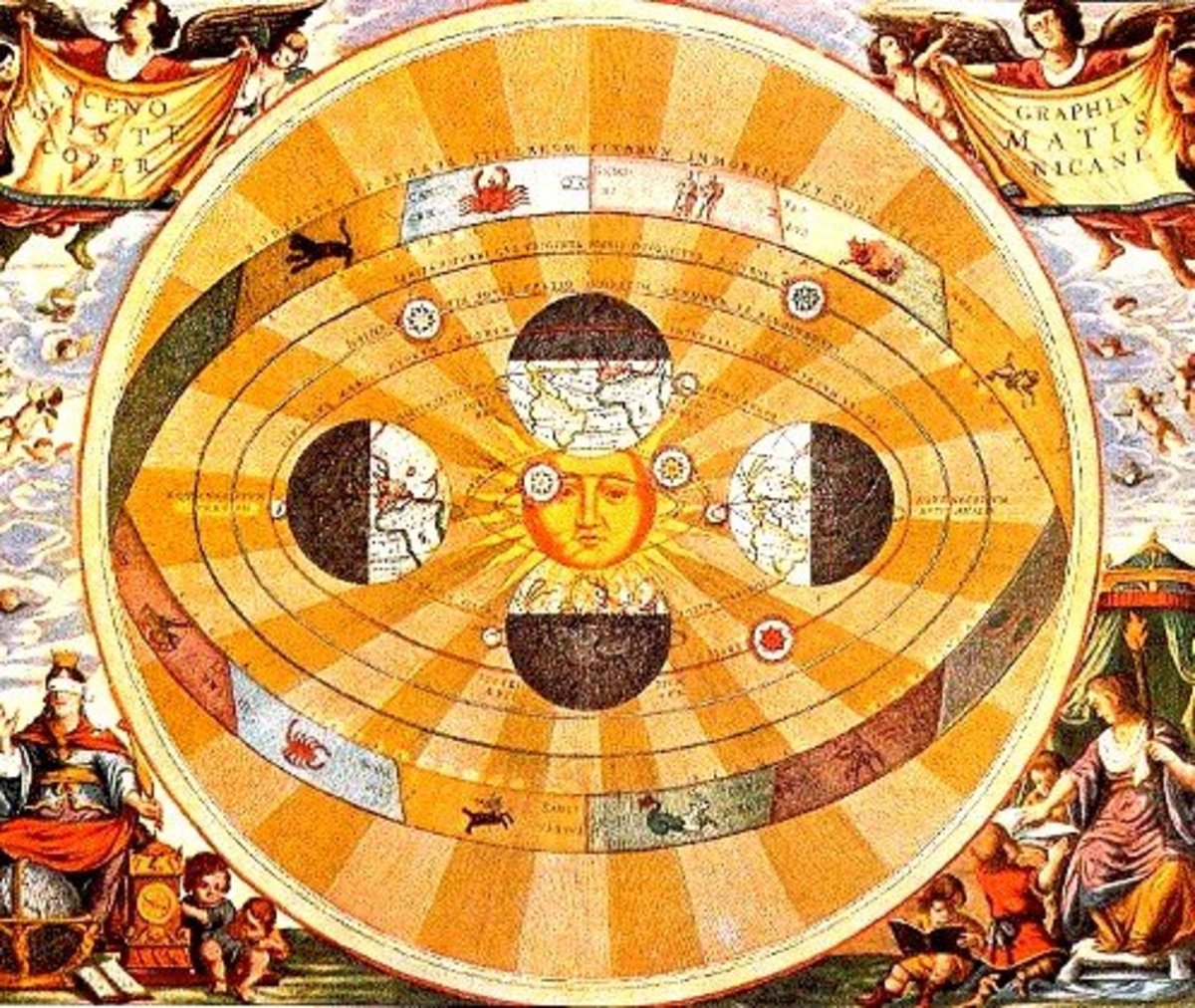
He affirmed the diurnal revolution of the earth on its axis; an assertion which is fully borne out by a quotation from one of his works, in a commentary on the "Brahmasphut'a-Siddhanta" of Brahmagupta by Prithudakaswami: "The Earth making a revolution produces a daily rising and setting of the stars and planets". At the same time he thought that this revolving of the earth was produced through the agency of a peculiar current of aerial fluid, or spiritus vector ("wind"), to which he assigned a distance of 150 yojanas (114 miles) from the surface of the earth. In opposition to the generally received opinion, he maintained that the moon, the primary planets, and the stars had no light of their own, and were only illumined by the sun; he consequently knew the true cause of solar and lunar eclipses.
Aryabhatta also ascribed to the epicycles, by which the motion of a planet is represented, a form varying from the circle and nearly elliptic. Moreover, he recognized a motion of the nodes and asides of all primary planets, as well as of the moon, and noticed the motion of the equinoctial and solstitial points, which he restricted, however, to an oscillation within the limits of twenty- four degrees, at the rate of one libration in seventy years. The length of AryabhatYa's sidereal year was 356 days 6 hours 12 minutes and 30 seconds. Aryabhatta stated the diameter of the earth at 1050 yojanas and its circumference at 3300 yojanas (25,080 miles). Hence it appears that he held the proportion of the diameter to the periphery of a circle to be seven to twenty-two, which is a nearer approximation than that of Brahmagupta and S'ridhara, who came after him.
The astronomical sects, of which Arabhatta is the reputed founder, were distinguished by the name of Audayakas, from Udaya, " rising;" implying that they fixed the beginning of the planetary motions on the meridian of Sri Lanka (Ceylon) at sun-rise, in opposition to the Arddharatrikas, who began the great astronomical cycle at midnight. Aryabhatta is the author of the " Aryasht'- as'ata" (eight hundred couplets in the Arya metre) and the "Das'agitika" (ten stanzas). The "Laghwarya-Siddhanta" is also ascribed to him: but, unfortunately, none of these works have yet been discovered; and we know them only through the numerous quotations from them, with which the works of subsequent writers abound. For an exposition of his numerical system and algebraic doctrine we refer to the article by another renowned scientist called BHASKARA.