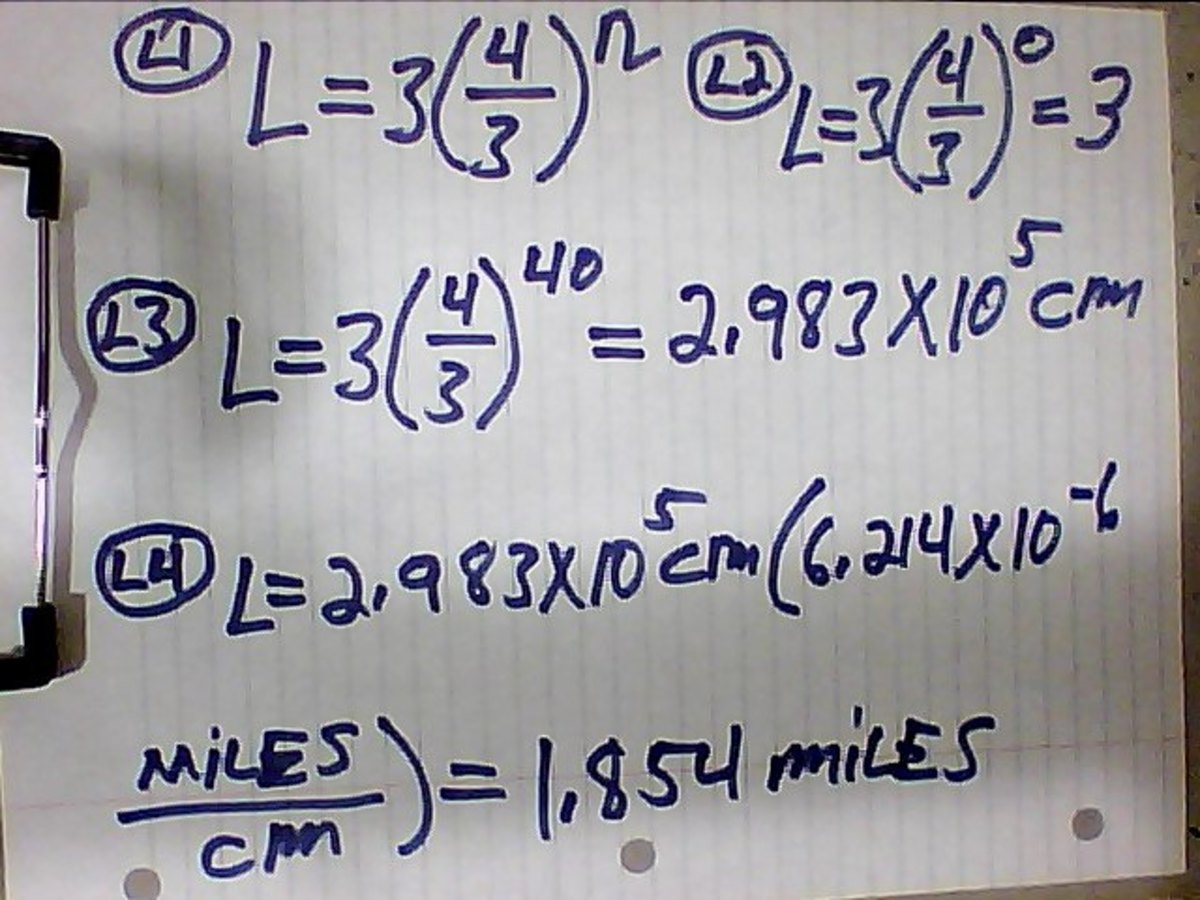Fractal Geometry
Fractal geometry is a field of mathematics whose actual boundaries are not yet entirely clear. Historically, its origins date back to early twentieth century and during the development of Measure Theory to the study of geometric sets seemingly paradoxical properties.
In these assemblies (Koch and Peano curves, Cantor set, Sierpinski triangle, etc..) Seemed to be a discrepancy between actual size and spatial configuration as a set of points (or area curves with infinite length between two points , etc.).
The term fractal was coined by B. B. Mandelbrot in 1977 (in his book The Fractal Geometry of Nature) to designate certain geometric objects irregular structure.Although Mandelbrot did not give a precise definition, fractals characterized by the following three properties:
a) Figures that repeat themselves infinitely often at different scales (self-similar sets.)
b) Figures with non-integer dimension (fractal dimension).
c) sets appearing after infinite iterative processes.
In his book, Mandelbrot defended the idea that eventually became the reason for the exponential growth of applications of fractals and the current popularization of the term: the forms of nature are fractals and multiple processes are governed by the same fractal behavior. Consider, for example at a border between states. Over time, this border is subject to change due to fighting, local agreements, small connections. That make it go the route of changing. The profile of a coast undergoes a process analogous to the border: the elements in contact, water and land, are subjected to long periods of interaction (wind and sea erosion, continental tilt, etc.) That permanently alter the shape of the coast . We study the fractal nature of various branches and trees, the drainage network of a river basin, the branching of the bronchi in the pulmonary alveoli ... Also are being used to transmit digital images fractals, or the stock market, where the fractal dimension provides the predictability of the phenomenon.
Obviously, fractals do not exist in reality and there are no lines or areas, but they serve to model real objects difficult to cover with the objects of Euclidean geometry.
The main difference between fractal geometry and classical geometry is that the latter has different contours, while the broken contours appear fractal geometry (undifferentiated), difficult to measure. For example, if it comes to measuring the contours of a country, the result depends on the resolution of the map, so a higher resolution means more length. It is for this reason that it will be measured using another type of fractal dimensions (fractal dimension), so you can compare the length of the coastline of a country to another.
In the early twentieth century appeared paradoxical sets with astonishing properties. These are the first examples of what we now call fractal
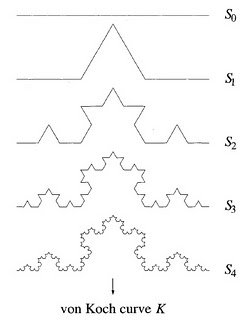
Koch curve
In 1904 Helge von Koch curve constructed that bears his name and has theproperty of having infinite length and it is not derivable in any of its points.
In its construction, is part of the unit segment [0.1] and is divided into three parts, replacing the central part of the two segments together with that party, would forman equilateral triangle. This gives a long traverse P1 4 / 3.
With each of the four segments repeats the operation described above, obtaining atraverse length P2 16 / 9. Proceed indefinitely in this way getting on a traversestage n Pn-length (4 / 3) n. The Koch curve is defined as the boundary curve to thesequence Pn converges when n tends to infinity.
Note that the length of the curve is infinite, then (4 / 3) n tends to infinity with n.Moreover, the length of the curve between two points on it is infinite.
The triangle and the Sierpinski tetrahedron
Around 1915, Waclaw Sierpinski constructed a set whose perimeter is infinite andzero area. Its construction is as follows. Starting with a triangle, draw a new trianglejoining the centers of their sides and removed from the initial figure. The result will be three triangles similar to the initial area (each) four times lower than the initial area. The operation is repeated with the three triangles and, in general, with thetriangles that will be formed. The result is the Sierpinski triangle.
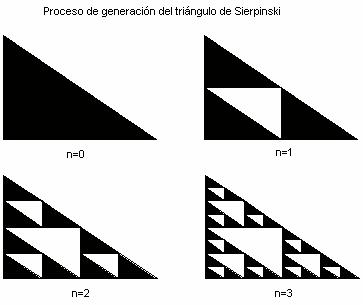
If the initial triangle has area 1, the first step will figure area 3 / 4, the second will be9 / 16, and in general, the figure will nth area (3 / 4) n. The Sierpinski triangle haszero area, then (3 / 4) n tends to zero as n tends to infinity. However, if the perimeterof the initial triangle is p, the first step is 3p / 2, the second 9p / 4, and in general thenth figure will have perimeter (3 / 2) np, so the perimeter of the Sierpinski triangle isinfinite, since (3 / 2) np tends to infinity with n.
The Sierpinski tetrahedron is constructed similarly. In a regular tetrahedron markthe midpoints of edges and tetrahedra are formed by joining them aside half.Removes the central figure. In each of the four remaining tetrahedra we repeat theprocess on.
The curves of Peano and Hilbert
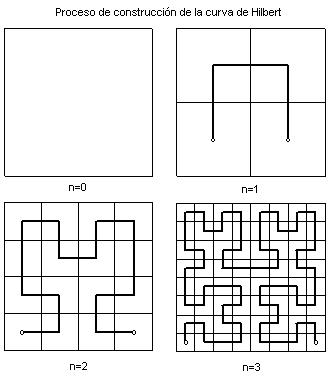
In 1890, Peano constructed a continuous curve passing through all points of theunit square [0,1] x [0.1]. It was the first example of a curve that "fills" space. Yearslater, Hilbert built the same type with a simple geometric construction described.
Hilbert curve is constructed as follows. Divide the unit square into four equal squares and join the centers of these squares by segment. Each of these squaresis divided again into four squares and connecting their centers always beginning with the lower left square and ending at the bottom right square. Continue in this way indefinitely joining the centers of the squares that are at each stage.
The limit of such polygonal curve "full" square drive and is called the Hilbert curve.
Below some examples of fractal geometry