Recurring Decimals. How to covert a recurring decimal into a fraction?

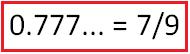
The method for converting a recurring decimal into a fraction is a little bit unusual. To do this you need to make some equations which eliminate the decimals. This is much easier to see if we carry out some examples.

Note: In the examples that follow the r means recurring, instead of a decimal point above the number which is the normal way to express a recurring decimal)

Example 1

Convert 0.7^r to a fraction (The r means that the 7 is recurring)

First make this recurring decimal equal to x:

x = 0.777... (Equation 1)

Next multiply both sides of the equation by 10:

10x = 7.777... (Equation 2)

The two equations can now be taken away so that the decimal parts are eliminated:

9x = 7

Next solve this equation which will give the values of x as a fraction instead of a decimal:

x = 7/9

Example 2

Convert 0.38^r to a fraction (The r means that the 8 is recurring)

First make this recurring decimal equal to x:

x = 0.3888... (Equation 1)

Next multiply both sides of the equation by 10:

10x = 3.888... (Equation 2)

If you take the two equations away the decimal part won’t be eliminated so you need to multiply by 10 again:

100x = 38.888... (Equation 3)

Now if you take the 3^rd and 2^nd equations away the decimal part of the numbers will be eliminated.

The two equations can now be taken away so that the decimal parts are eliminated:

90x = 35

Next solve this equation which will give the values of x as a fraction instead of a decimal:

x = 35/90 which simplifies to 7/18

Let’s take a look at 1 last example.

Example 3

Change 2.36^r1^r into a fraction

The r means the 6 is repeating and similarly for the 1. So you have:

x = 2.3616161...

Convert 0.38^r to a fraction (The r means that the 8 is recurring)

Next multiply both sides of the equation by 10:

10x = 23.616161... (Equation 2)

If you take the two equations away the decimal part won’t be eliminated so you need to multiply by 10 again:

100x = 236.16161... (Equation 3)

And still the decimal parts cannot be eliminated by subtracting any of the above equations so you need to multiply by 10 again:

1000x = 2361.616161...(Equation 4)

Now the decimals match in equations 2 and 4. So these can be subtracted to give:

990x = 2338

Next solve this equation which will give the values of x as a fraction instead of a decimal:

x = 2338/990 which simplifies to 1169/495

To summarise, all you need to remember is to make x equal the recurring decimal and keep multiplying this by 10 until you can subtract any of the 2 equations so that the decimals will eliminate.