Right Triangle Trigonometry Part 2

Sine, Cosine and Tangent
Sine, Cosine and Tangent are three trigonometric functions. Each of these functions describes the ratio associated with a given angle, as a numeric value. Sine describes a ratio of the length of the side opposite an angle to the length of the hypotenuse of the triangle. Cosine describes a ratio of the length of the side adjacent to an angle to the length of the hypotenuse of the triangle. Tangent describes a ratio of the length of the side opposite an angle to the length of the side adjacent to the angle.
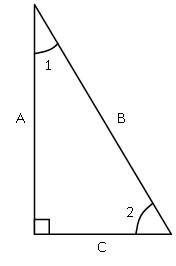
Six Trigonometric Ratios
The following six ratios will describe the triangle pictured in Fig. 1
- The sine of angle 1 is equal to the ratio of opposite side C to the hypotenuse B
- The cosine of angle 1 is equal to the ratio of adjacent side A to the hypotenuse B
- The tangent of angle 1 is equal to the ration of opposite side C to the adjacent side A
- The sine of angle 2 is equal to the ratio of opposite side A to the hypotenuse B
- The cosine of angle 2 is equal to the ratio of adjacent side C to the hypotenuse B
- The tangent of angle 1 is equal to the ration of opposite side A to the adjacent side C
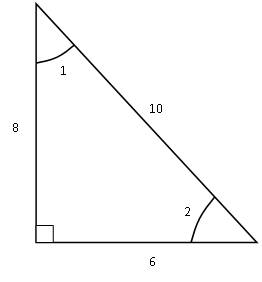
Six Trigonometric Ratios
Referencing the triangle in Fig. 2, values will now be used to describe the relationships of the sides and angles.
- The sine of angle 1 is equal to 6:10 or 0.60 (6/10)
- The cosine of angle 1 is equal to 8:10 or 0.80 (8/10)
- The tangent of angle 1 is equal to 6:8 or 0.75 (6/8)
- The sine of angle 2 is equal to 8:10 or 0.80 (8/10)
- The cosine of angle 2 is equal to 6:10 or 0.60 (6/10)
- The tangent of angle 2 is equal to 8:6 or 1.33 (8/6)
The numeric values associated with angles 1 and 2 can now be used to find the actual size of the angles. Up to this point, angles 1 and 2 have not been assigned an angular value. All that is known about the size of the angles is that they must have a sum of 90°. Remember, that the sum of all the angles must be 180°. Since one of the angles remains 90°, angles 1 and 2 comprise the difference (90°).




