- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming
Find the Roots of equation by Newton Raphson Method via C Programming
Vote time :
Does C Programming generates interest in you ?
Newton Raphson Method
Newton's Method is mainly used for finding the roots of a polynomial. This method is also known as Newton Raphson method in the numerical analysis. We start with our approximated root of a function in this method which further computes the better approximation which is somewhere near the actual root.
Newton Raphson Method is also known as Method of tangents. Let us now demonstrate how to use this program:
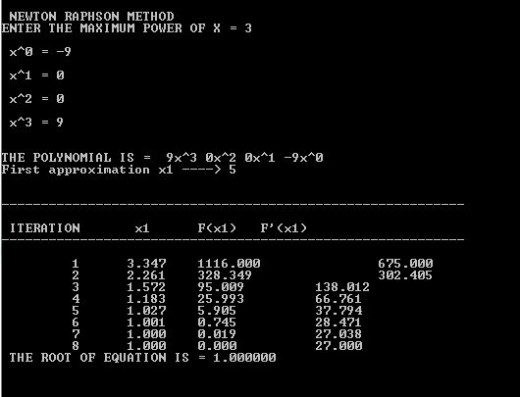
Consider an example : f(x)=9x^3-9 . we need to find root of this polynomial and we assume its root to be 5. Now, max power of x will be 3 , x^0 = -9 , x^1 = 0 , x^2 = 0, x^3 = 9 and first approximation = 5 . After entering such details according to our polynomial , Newton Raphson C Program will display the root of polynomial and iterations as the output.
C Program Source code of Newton Raphson Method
#include<conio.h>
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int maxpow,i=0,cnt=0,flag=0;
int coef[10]={0};
float x1=0,x2=0,t=0;
float fx1=0,fdx1=0;
int main()
{
printf("\n NEWTON RAPHSON METHOD");
printf("\nENTER THE MAXIMUM POWER OF X = ");
scanf("%d",&maxpow);
for(i=0;i<=maxpow;i++)
{
printf("\n x^%d = ",i);
scanf("%d",&coef[i]);
}
printf("\n");
printf("\nYour polynomial is = ");
for(i=maxpow;i>=0;i--)
{
printf(" %dx^%d",coef[i],i);
}
printf("\nFirst approximation x1 ----> ");
scanf("%f",&x1);
printf("\n\n---------------------------------------\n");
printf("\n Iteration \t x1 \t F(x1) \t \tF'(x1) ");
printf("\n------------------------------------------\n");
do
{
cnt++;
fx1=fdx1=0;
for(i=maxpow;i>=1;i--)
{
fx1+=coef[i] * (pow(x1,i)) ;
}
fx1+=coef[0];
for(i=maxpow;i>=0;i--)
{
fdx1+=coef[i]* (i*pow(x1,(i-1)));
}
t=x2;
x2=(x1-(fx1/fdx1));
x1=x2;
printf("\n\t %d \t%.3f \t %.3f\t\t%.3f ",cnt,x2,fx1,fdx1);
}while((fabs(t - x1))>=0.0001);
printf("\n THE ROOT OF EQUATION IS = %f",x2);
getch();
}