- HubPages»
- Technology»
- Computers & Software»
- Computer Science & Programming»
- Computer Programming Tutorials
Intro to Java Programming: Using Recursion to Solve Factorial Problems
There are four main mathematical problems that a programming class will cover as it pertains to the study of recursion and they are factorials, the Fibonacci sequence, the Towers of Hanoi, and fractals. The reason these mathematical methods are used in the study of recursion is the fact that all have a base case and are exponential. Indeed, the exponential part is the key since it forces a programmer to create a function or class that has to make multiple calls to itself.
In this hub, I will show you how to create a recursion class that can calculate factorials in the Java programming language. I will also introduce a built in Java class known as BigInteger which gives a programmer the ability to accept large integer numbers as they are returned to the main program. However, before we get into the code, I would like to explain what are factorials.
What Are Factorials?
In mathematics, a factorial of a non-negative integer, denoted as n!, is the product of all integers less that or equal to n. For example to figure out the product of the factorial of 5 aka 5!, you would have to multiply all numbers starting with 5 down to 1 like so: 5 x 4 x 3 x 2 x 1 = 120. So, the product of the factorial of 5! = 120 whereas n! = n x (n – 1).
Factorials also have something called a base case which are 0 and 1 or 0! and 1! respectively. These two numbers will always equal 1 and when reached signifies the last numbers that need to be multiplied to find the final product.
So, with that said, here is the code.
Code: Factorial Calculator
//********************************************************************
//Recursive Factorial Method
//
// Version 1
// Created by Bink
//********************************************************************
package factorialcalculatorver1;
import java.math.BigInteger;
public class FactorialCalculatorVer1 {
//recursive method factorial (assumes parameter is >= 0
public static BigInteger factorial(BigInteger number) {
if(number.compareTo(BigInteger.ONE)<=0)//Test Base Case
return BigInteger.ONE;//if base case is 0! = 1 or 1! =1
else //do recursive step
return number.multiply(factorial(number.subtract(BigInteger.ONE)));
}
public static void main(String[] args) {
//Calculate the Factorial of 0 to 50
for(int counter = 0; counter <= 50; counter++)
System.out.printf("%d = %d\n",counter,factorial(BigInteger.valueOf(counter)));
}//end main
}//end class
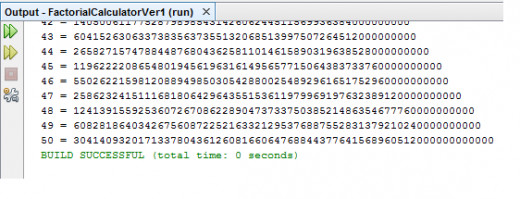
Now run the code and you should get the following from the output window:
Output Window in NetBeans IDE
Code Explained:
As I stated earlier, I decided to use the BigInteger class which is a built in class in Java. Well at least as of version 7 and 8 if the JAVA SE SDK. I like to use it because it allows me to pass large integers into a class or function. I also like it because it has a method (BigInteger.ONE) that is perfect to test for the base case and in turn allows the recursive loop to end. To use the BigInteger class you have to import it. So, the first line of code under package is an import (java.math.BigInteger) which allows you to use this java class.
Next you have the programs start up class (FactorialCalcualtorVer1) which is the exact name you used when you initially created the program. Java is a very object oriented programming language so you will always have a start up class.
The next class is the class that actually does the computations. It is declared public and static because we want to be able to access this class when the program runs (public) and we want to make sure that the number that is returned back to the main class or program is not erased from memory (static). In fact, any class that uses the static keyword will make sure that any value it contains will remain throughout the life of the program.
Within this class you see an if/then/else statement. This is where the number that the class brings in as an argument is compared and then if it is not 0 or 1 then the multiplication takes place and the number is returned. If the number that comes in is 0 or 1, then BigInteger.ONE is returned and the recursive step ends.
Finally, there is the main class that prints out the results to the output window. It uses a for/next loop and the variable counter. During this loop the System (printf) method is used which allows the product of the factorials 0! to 50! to be printed out. It also makes a call to the factorial class on each pass that allows the class to do its computation on each value of counter. This is why the program is a recursive program because at each pas of the for loop, the class factorial is actually making a call on itself.
Conclusion:
So, there it is. Again as stated earlier this one of four methods I use to show how to create a recursion type of program. The next method I will show is the Fibonacci sequence. If you want to see the next method then click here.
Related
Programming in Java Netbeans - A Step by Step Tutorial for Beginners: Lesson 26
Programming in Java Netbeans - A Step by Step Tutorial for Beginners: Lesson 30
Programming in Java Netbeans - A Step by Step Tutorial for Beginners: Lesson 27
Programming in Java Netbeans - A Step by Step Tutorial for Beginners: Lesson 8
Programming in Java Netbeans - A Step by Step Tutorial for Beginners: Lesson 35
