What is the formula for finding the volume (capacity) of a cylinder or tin?

The volume of a cylinder can be found by working out the area of the circle at the end of the cylinder using A = πr² (also referred as the cross-sectional area) and multiply this answer by the length of the cylinder. Therefore:

Volume = Cross sectional area × Length

V = πr² × l

V = πlr²

So if you have the radius and length of the cylinder then all you need to is substitute these into the formula V = πlr².

Example 1

Work out the volume of the cylinder below:

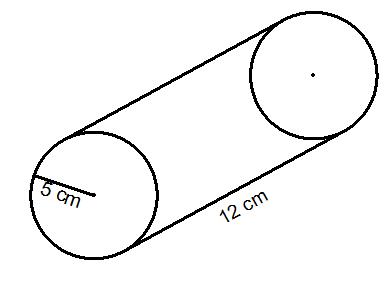
Here the radius of the cylinder is 5cm and the length of the cylinder is 12cm:

So r = 5cm and l = 12cm

First work out the area of the circle:

A = πr²

A = π × 5²

A= 78.5...cm²

Leave this answer on your calculator and multiply it by the length to give the volume:

V = 78.5... × 12

= 942 cm³ to the nearest whole unit

Alternatively, you can substitute r = 5 and l = 12 directly into V = πlr²

V = πlr²

V = π × 12 × 5²

V = 942 cm³

Example 2

Work out the volume of the cylinder below:

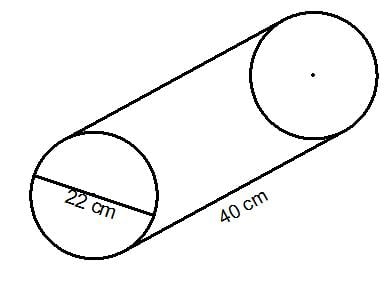
Here the diameter of the cylinder is 22cm and the length of the cylinder is 40cm.

Notice that you are given the diameter of the circle and not the radius of the circle so you need to halve the diameter to give the radius:

So r = 11cm and l = 40cm

First work out the area of the circle:

A = πr²

A = π × 11²

A= 380.1...cm²

Leave this answer on your calculator and multiply it by the length to give the volume:

V = 380.1... × 40

= 15205 cm³ to the nearest whole unit

Alternatively, you can substitute r = 11 and l = 40 directly into V = πlr²

V = πlr²

V = π × 40 × 11²

V = 15205 cm³

Example 3

A tin of soup has a radius of 2 inches and a height of 5 inches. Work out the volume of soup in the tin.

Here r = 2 and l = 5. This time let’s just substitute r = 2 and l = 5 into V = πlr²:

V = πlr²

V = π × 5 × 2²

V = 62.8 cm³ rounded to the nearest tenth.