Achieving the Flexibility/Maintainability quality attributes in WCF Services
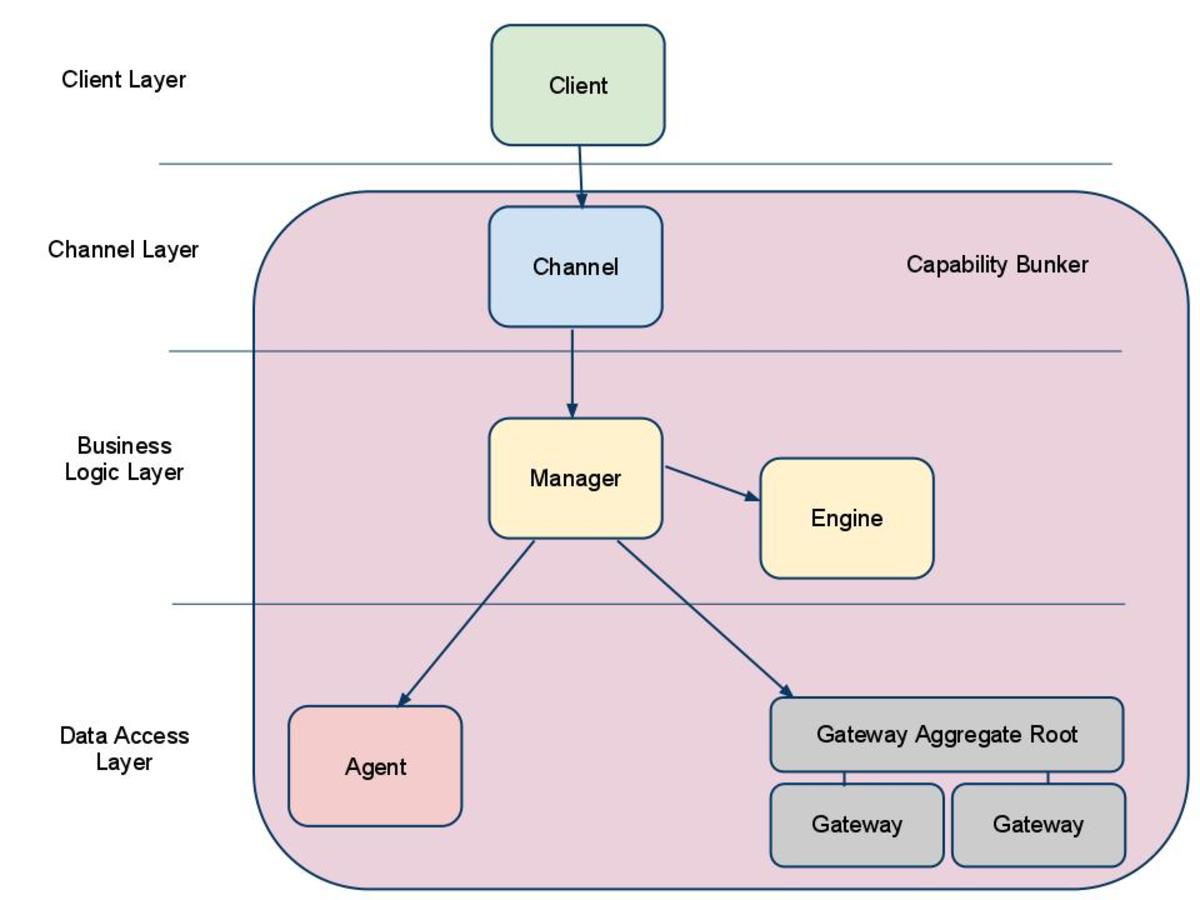
Manager, Engine, Gateway, a SOA Model
This article is the second in a series that offers practical advice to the creators of complex software systems on how to achieve the non-functional or technical requirements of their project.
Service orientation (SO) is not easy, but as a methodology, to the best of our knowledge as an industry, offers the best solution for building complex software systems.
SOA books describe the methodology, and the technology but seldom do they give any practical advice for building these types of systems. Here is some real no nonsense advice from the trenches for development.
It builds upon this article the introduces the model and this one that introduces the topic, I suggest you read these two articles first as they will set the context for what follows.
Flexibility
Flexibility is the ability of a system to adapt to varying environments
and situations, and to cope with changes to business policies and rules.
A flexible system is one that is easy to reconfigure or adapt
in response to different user and system requirements. The intentional
separation of concerns between the manger and engine components aids
flexibility as only a very small piece of the system is affected when
policies or rules change. Engines encapsulate rules, and mangers
workflow, so if the how we do something changes, only manager’s change,
if the rules around the process change, only engines change.
As a
general heuristic we say that engines and gateways should be reused.
This means that the strategy and the data access should be written once
and reused as much as possible. It is then possible to reconfigure the
solution per use case (manager) by picking the engines and gateways
required.
This becomes productive when you need to provide new
functionality, which is conceptually just more use cases, that use the
existing data in new ways, you only need to write a new manager and
reuse the gateways and engines. If you need to reuse a manager, it means
you have two identical use cases, eliminate one and delegate
functionality to the existing service, never copy and re-host a manager.
This is the reason we introduced the concept of the aggregate
root and a gateway per contract, so that even if you require a different
view of the data you will be able to aggregate existing gateways to
produce the contract that you require.
Maintainability
Maintainability is the ability of a system to undergo changes to its
components, services, features, and interfaces as may be required when
adding or changing the functionality, fixing errors, and meeting new
business requirements. The maintainability of a system is dependent on
its ability to manage complexity.
In reality as it turns out, it
is not complexity that causes maintenance headaches, but rather how the
complexity is sequestered or partitioned. Complex code that is well
partitioned and lives in one place only is easy to
manage, and when a simpler method is found it is easy to remove
and replace. Complex code that is scattered over many
places with multiple dependencies to other pieces of
dependent code equals maintenance nightmare.
So the question is;
how to partition our application so that we can avoid complexity from
spreading. Luckily the answer lies in the realm of set theory and
equivalence relations.
In order to manage complexity we must first
understand it, the complexity of a system is a function of the number of
states in which a system can find it’s self.
An example is a system (A) that has 3 dice, so the number of potential states is 63 or 216 potential states. Another system (B) with one dice has 61or
6 potential states, if you where to make repeated guesses for both
systems, you would be right, on average 36 times more often with B than
you would be with system A because system B is less complex and easier
to predict.
With this basic model of complexity, we can gain
some insight into how complexity can be better organized. Consider
another two systems (C) and (D) both have three six sided dice, but in C
all the dice are together as before, but in D the dice are divided
into three partitions. Let’s assume we can deal with the three
partitions independently, in effect, three subsystems each like B. We
know that the complexity of C is 216. The overall complexity of system D
is the sum of the complexity of each partition (61 + 61 + 61)
or 18. If you are not convinced of this imagine inspecting C and D for
correctness in C you would need to examine 216 different states,
checking each for correctness. In system D you would need to examine
only 6 states in each partition.
Complexity
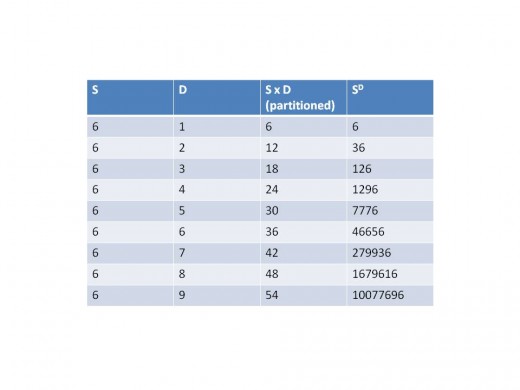
The above table demonstrates how much more complex a non-partitioned system of 9 dice is compared to a partitioned system containing the same number of dice. Ratio of 10,077,696 to 54, a lot!
How then do we partition a software system so we too can gain the advantage from this property of the universe?
A partition is a concept from set theory; a partition is a set of sub sets that divide a larger set so that all the items in the larger set live in one, and only one of the subsets. Like our dice example each die lives in one and only one bucket. One can also observe that in any set of items there are at least N possible ways to partition that set.
In software systems it just isn’t enough to just partition variables into different subsets; we need to find one that honours the dependencies between the variables.
This is where equivalence relations become useful. An equivalence relation is a Boolean (true/false) binary relation that for any elements, say a, b, c in the same set the following three properties are always true:
E(a,a) is always true – reflexivity
E(a,b) always implies E(b,a) – symmetry
E(a,b) and E(b, c) always implies E(a, c) – transitivity
Consider a small shop, all the items in the shop can be considered as being in the same set, if we pick the equivalence relation costs the same as let’s see how this becomes useful.
The shop stocks Cereal for R10.00, Pens for R10.00, Coke R10.00, and Notebooks R20.00.
Reflexivity – costs the same as (Pens, Pens) = true
Symmetry - costs the same as (Cereal, Pens) = true and costs the same as (Pens, Cereal) = true
Transitivity - costs the same as (Cereal, Pens) = true and costs the same as (Pens, Coke) = true and costs the same as (Cereal, Coke) = true
And to check our logic costs the same as (Cereal, Notebooks) = false.
Thus because for a particular equivalence relation every item in the set lives in only one partition we can use equivalence relations to formulate partitions. In formulating architecture the equivalence relation that is of most interest to us is synergy, two functions are synergistic when one requires the other to be effective, if you can imagine a situation when one can be used without the other they are said to be autonomous.
Equivalence in Practice
In practice we take our system and pull out all the required functionality for example in a retail operation use cases could be:
Calculate total cost,
Calculate change,
Charge credit card,
Remove from stock,
Stock report
If
we apply the synergy test we can we that Calculate total cost is
synergistic with Calculate change, it is hard to imagine one without the
other, in our retail set. At first glance Charge credit card looks
synergistic with Calculate total cost, but remember symmetry, it is a
two way street; it is possible to imagine a scenario where you would
Calculate total cost without charging credit cards (cash payment for
example), therefore Charge credit card is actually autonomous to
Calculate total cost.
Another property of equivalence relations
is that although the inverse of an equivalence relation is never itself
an equivalence relation it has some interesting mathematical properties
of its own. If we denote E as an equivalence relation and its inverse as
~E, if E was used to generate a partition, the following could be said:
If a and b are in the same equivalence class of E then ~E(a, b)
is always false, and if a and b are in different equivalence classes of
E then ~E(a, b) is always false.
For example, costs the same as
(Cereal, Pens) = true, think of this as E(a, b), and does not cost the
same as (Cereal, Pens) = false, then this is ~E(a, b) because these two
items are in the same equivalence class of items that cost ten rand.
Similarly ~E(Pens, Notebooks) = true.
This leads to a useful
trick, as you can see it is quite difficult to generate such a set where
does not cost the same is false for all elements within a set and true
for all elements across sets, but if you realize that does not cost the
same is the inverse of costs the same the exercise becomes trivial and
you will automatically have the property of non-equivalence for does not
cost the same. So why is all of this so important? Well in designing
service orientated applications synergy is not a particularly important
property, but its inverse autonomy is a very important one, so important
it is included as a SOA tenant.
Five Laws of Partitions
So with this incredibly useful method to partition application
functionality we also get the best possible partition and achieve the
tenet of autonomy, our system is a small as it needs to be no smaller.
The rules to formulating partitions can be summarized into five laws:
- Partitions must be true partitions. Items live in one partition only, ever.
- Partitions must be appropriate to the problem at hand. Partitions only minimize complexity when they are appropriate to the problem at hand, e.g. a clothing store organized by color would have little value to customers looking for what they want.
- The number of subsets must be appropriate. Studies show that there seems to be an optimum number of items in a subset, adding more subsets, thus reducing the number of items in each subset, has very little effect on complexity, but educing the number of subsets, thus increasing the number of elements in each subset seems to add to complexity. The number seems to sit in the range 3 – 12, with 3 – 5 being optimal.
- The size of the subsets must be roughly equal. The size of the subsets and their importance in the overall partition must be roughly equivalent.
- The interaction between the subsets must be minimal and well defined. A reduction in complexity is dependent on minimizing both the number and nature of interactions between subsets of the partition.
By reducing complexity and ensuring that our applications are well partitioned and autonomous we effectively sequester complexity and make our systems maintainable