Basic trigonometry
Soak a What?
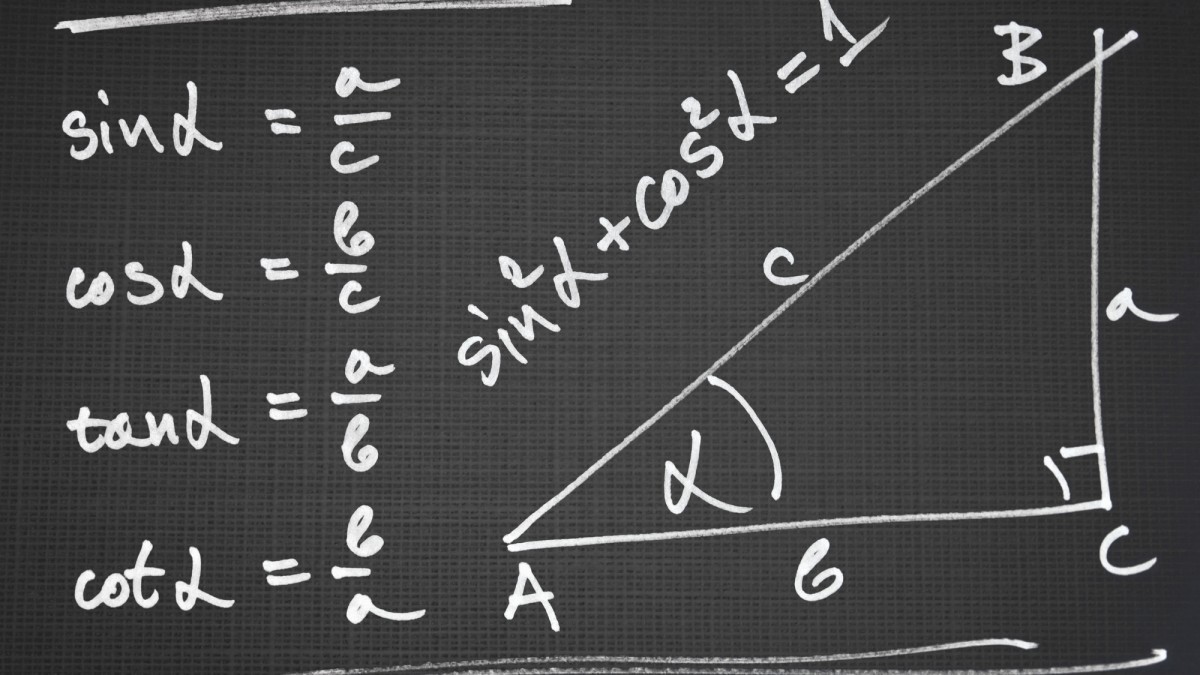
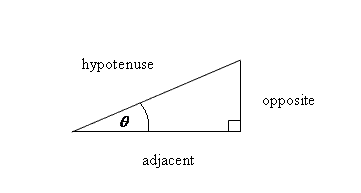
Sine is opposite over hypotenuse; Cosine is adjacent over hypotenuse; Tangent is opposite over hypotenuse.............or "soh cah toa" I am not a big fan of this memory enhancer but this is what is being taught and it works.
So what does this mean?
Lets look at sine first and we will just call this sin θ. This will be used to solve various components of right triangles. (Now, of course trigonometry is not just for right triangles but that is where we will start.)
If we have a triangle with an angle θ, then the operation sin θ=(opposite leg)/hypotenuse. If we let the opposite =4 cm and the hypotenuse=5 cm, then sin θ=4/5 or .8.
Okay not too bad right?
Cosine or cos θ=(adjacent leg)/hypotenuse. We know by the Pythagorean theorem (or if we know our special triangles) that the adjacent leg = 3 cm. (hyp^2-opp^2)^1/2=adj. Therefore cos θ= 3/5 or .6.
Now tangent or tan θ =(opposite leg)/ (adjacent leg)=4/3 or 1.33.
By knowing sin θ, we were able to determine both cos θ and tan θ.
Lets do one more. We have a right triangle and the tan θ=2. This means we can let the opposite leg = 2 and the adjacent leg =1 and the hypotenuse would equal (1^2+2^2)^1/2=(1+4)^1/2=5^1/2=2.24. This is all just a ratio so we could have let the opposite=4 and the adjacent=2 and the hypotenuse=4.48 but 2 and 1 respectively are a little easier to use.
sin θ=opp/hyp=2/2.24=.89
cos θ=adj/hyp=1/2.24=.45
If you have a triangle and know either sin θ, cos θ, or tan θ, you can figure out the other 2.
This is a very basic discussion of trigonometry. Trigonometry as it applies to right triangles is a relationship between angles and lengths of sides. This can be used in construction like figuring cutting angles for trusses on a slopped roof. One can figure ballistics of a projectile and this gives us a horizontal and vertical component. Trigonometry is actually a very useful math methodology.
In the next basic trigonometry post, I am going to explain how lengths of sides and angles relate to each other. I would love to hear your comments and I hope that I am explaining this in a way that most people can understand. I would love to help anyone who would like to learn math. That is my intent.
Before I end this post, I will give the other three trigonometry functions. The first three explain every side of a triangle but the following functions find their use in both proofs as well as calculus solutions so it is good to know and they are easy to learn.
Secant or sec θ=hyp/adj=1/cos θ.
Cosecant or csc θ=hyp/opp=1/sin θ.
Cotangent or cot θ= adj/hyp=1/tan θ.
sha cho cah? Hey that doesn't sound to good.
Post note: All numbers are rounded to 2 significant digits.