Zero is not a Perfect Happy Number

Happy Numbers
A Happy Number is a number that satisfies the following condition. If you square its digits, add them together, and then take the result and square its digits and add them together, and keep doing that over and over again, you come down to the number 1. eg. 32.
32: 32 + 22 = 9 + 4 = 13
13: 12 + 32 = 1 + 9 = 10
10: 12 + 02 = 1 + 0 = 1
The happy numbers below 500 are
1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496.
Perfect Numbers
What is a Perfect Number?
One that is the sum of all its divisors excluding itself.
For example, consider the number 6. Its divisors are 1, 2, 3 and 6.
Leaving 6, sum of all its divisors = 1 + 2 + 3 = 6. So 6 is a perfect number.
Examples: 6 (1+2+3), 28 (1+2+4+7+14), 496, 8128, etc., are perfect numbers.
A perfect number is a number that is half the sum of all of its positive divisors.
Number Theory
Zero
0 is a number to represent nothing. 0 is an integer between -1 and 1. 0 is neither positive nor negative. 0 is an even number as it is divisible by 2. 0 is used as a placeholder in place value system. 0 is the additive identity of Integers and Reals in Algebra.
The concept of zero as a number and not merely a symbol for separation is attributed to India. The Sanskrit word Shunya was used in Indian Texts to refer the concept of void. The oldest known text using a zero is the Jain text Lokavibhaga from India dated 458 AD. An early documented use of the zero by Indian Mathematician Brahmagupta in his work dates to 628 AD. He treated zero as a number and explained operations involving it, including division. In 9th century AD, practical calculations were carried out using zero, treating like any other number, even in the operation division. The first known use of a symbol for the digit zero, a small circle, appears on a stone inscription found at the Chaturbhuja Temple at Gwalior in India, dated 876 AD.
The Hindu-Arabic numerals and the positional number system were introduced in 825 AD by a Persian Mathematician Muḥammad ibn Mūsā al-Khwārizmī from Baghdad in his book titled al-Kitab al-mukhtasar fi hisab al-jabr wa'l-muqabala. This book summarised Greek and Hindu knowledge and also contained his contributions to mathematics including an explanation of the use of zero. So we can conclude that zero was introduced by Indians.
- Fun in class room
Time spent laughing is time spent with the gods says a Chinese proverb. Q: Why is the Math book very sad? A: Because it has too many problems! Q: Why did Robinhood only rob the rich? A:...
- Fun with Numbers - Jokes
A good mathematical joke is better, and better mathematics, than a dozen mediocre papers.- J. E. Littlewood. Philosophy is a game with objectives and no rules. Mathematics is a game with rules and no...
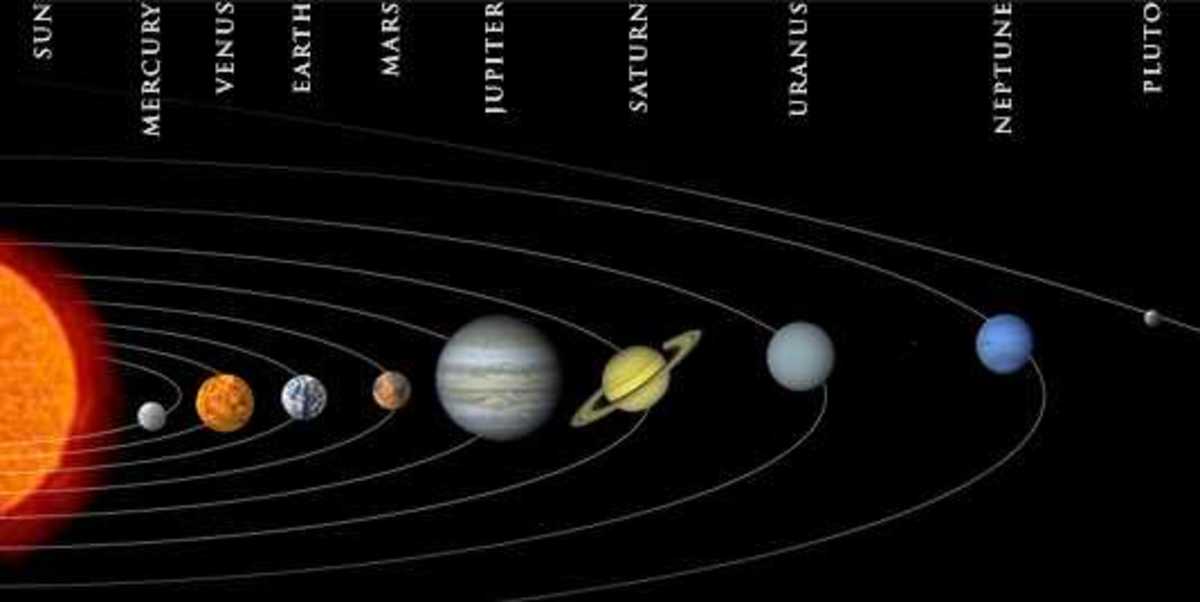
- Fun with Numbers - Astronomy
In 1768, Bode published his law giving the distances of the planets from the Sun in terms of the distance of Earth. Consider the series 0, 1, 2, 4, 8, 16, 32, 64, 128, 256, .. Multiply by 3, ...
- Vailankanni My Pilgrimage Center
We visit Vailankanni every year from the nearest airport at Tiruchy (154 kms). No words can express the happiness and peace that we feel in the presence of our beloved Mother. Vailankanni, a hamlet on...