Teaching elementary multiplication to kids; How to teach primary school math
A long train journey, a young student and the number 49
A little while ago I was catching the train home to visit my parents during my university break. Not long before reaching my destination, my phone battery died and I had to suffer the last boring 15 minutes without music. It's was far from boring.
To my left I noticed a girl of maybe 7 or 8 going over her seven-times tables with her Grandma. It went something like the following:
"Not yet, you have to do them now. What's 7x7?"
*I watch the girls expression as she clearly delves through the depths of her mind for the memorised answer*
"48"
*Her friend across from her looks up from her book*
"It's 49"
"my teacher said it's 48"
*I contemplate whether to say something. May as well*
"Would you like to know the easy way to do your times tables?"
It's a shame I only had 10 minutes to try to explain what I'm going to explain in this article, but I think I at least got her started on the right path, or curious enough that she can figure the rest out on her own. Asking someone what 7 x 13 is usually gets them thinking and it's and easy one to explain. She could do 7 x 10 easily, 7 x 3 easily and 70 + 21 easily but she struggled to complete 7 x 7 or 7 x 13. The following is what I would have liked to teach her, as best as I can explain it.
In the beginning...
In the beginning, mathematical "tricks" were created.
This made a lot of mathematicians very angry and has been widely regarded as a bad move. Ok so it's not that bad and they can be very useful; but there is one serious flaw. You see, these "tricks" allow people to get from the question to the answer without truly understanding how they got there. That's not so bad, until it is presented on the forefront of a learning environment.
When I was in primary school, my peers and I were taught to memorise the result of every times table from 1x1 to 12 x 12 and nothing more. For anything more complicated, I was taught to use the common process on paper.
When I was in high school I was taught little tricks like: Simplify: 2a = 4b. "remove 2 from each side" a = 2b. This is of course the correct answer, but the concept isn't explained. You can get the answer by thinking: well if 2a and 4b are two copies of the same circle then "a" is half that circle and "b" is a quarter of that circle. Logically 2 "b"s make one "a" so therefore a = 2b. This is a much healthier way of solving the problem, at least before the tricks are learned; because it teaches a real understanding of what is happening. Afterwards the tricks can be helpful to speed up the process.
Now I wasn't a stupid child, but i had a bit of trouble remembering the answers to 144 questions. I still have trouble remembering stuff for straight forward question-answer exams. I still can't instantly tell you the answer to 8 x 6 by memory. I can however, figure it out in the time it takes you to retrieve it from memory. I could figure out 26 x 12 in the same time. In my head. I could do this when I was 6, I'll be doing it when I'm 106 and I hope you will be doing it when you're 106 (cross fingers for us).
In the video below Richard Feynman expresses the problems associated with a standardised learning system in mathematics.
R. P. Feynman on Algebra

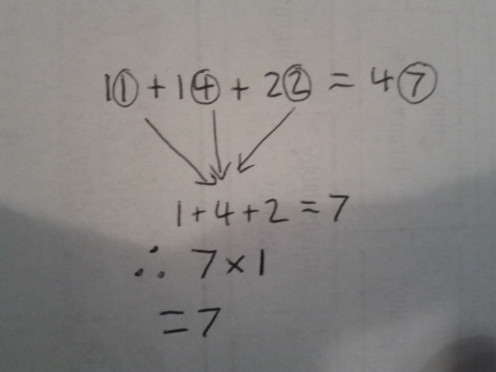
How to do Addition in your head
Addition is the first step to using any number system. It's the easiest step, the one most people know and the one most people are competent with. It can be a little tricky though. The more numbers you have to add together and the variability of those numbers can make it difficult to do in your head. Take 11 + 14 + 22. This is an easy one. The best way to do it isn't to add 11+ 14 and then add 22. If you do this, the sum will take much longer to work out as more numbers are added.
The best way is to do it in Two stages. First add your 10's column together. This is 10 + 10 + 20 = 40. Remember 40.
Next you ad your 1's column. This is 1 + 4 + 2 = 7. Add 7 to the previously found 40 and you have your answer. 40 + 7 = 47.
The sums 10 + 10 + 20 and 1 + 4 + 2 and 40 + 7 are much easier to work out than 11 + 14 + 22.
If it takes (for example only) 10 seconds to work out 11 + 14 + 22 and only 2 seconds to work out each of the other three, then the method I have just explained is not only easier but also faster.
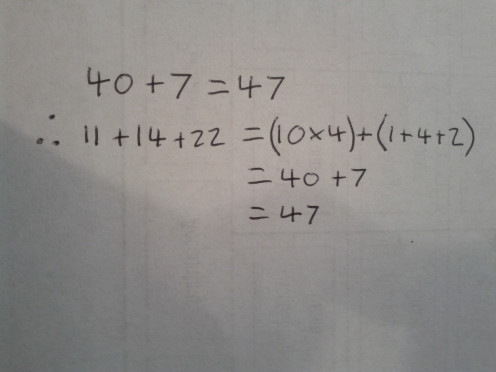
You can speed this process up if you attack it from a multiplication standpoint. 10+10+20 is the same as 10 x 4 which is marginally faster to work out in this case. In more complicated examples the time gap would be much larger.
If I had the sum: 10 + 33 + 11 + 49 + 8
I would do it this way:
*Count the 10's column and x by 10*
=10 x 9 + 3 + 1 + 9 + 8
*Add together the easy parts of the addition*
= 10 x 10 + 3+ 8
*Add the remaining addition to find the final result*
= 111
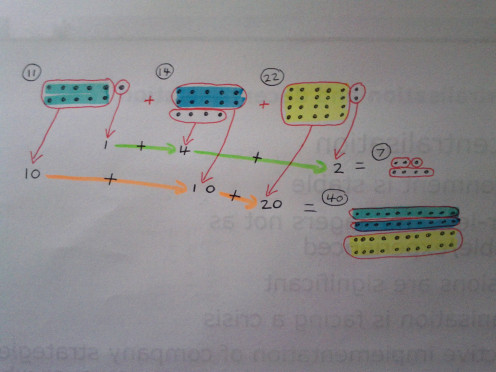
I have drawn the above picture to express the fact that all we are doing is moving around the units that make up the equation 11 + 14 + 22 = 47.
We are given clumps of 11, 14 and 22, and mix and match the dots in them to make new clumps that make more sense to the human brain (which of course will be different depending on the individual).
If you so wished, you could change it to 13 + 10 +24 if this was what you preferred. As long as no individual units are added or removed, the answer will always of course be 47.


Subtraction in your head
Subtraction works largely the same as addition. All I have done here is take 2 from the 4 we are subtracting and add it to the 18 we are subtracting We are still subtracting a total of 22 but the two step in which we do it are different. On paper this process seems pointless but removing 20 from 73 and then 2 is much easier in your head than removing 18 from 73 and then 4. When you are trying to larger, more complicated sums, this comes in handy.


In this diagram I am trying to show that you can change the original pool of units you are subtracting from as long as you change how much you are subtracting from it as well.
If our original question is 73 - 18 - 4 and we change it to 73 - 22, we can change the entire question to 71 - 20 because 71 - 20 = 73 - 22. In both cases the answer is 51. This is what is happening in the commonly taught algebra trick when simplifying. Though it's subtract 2 from both sides of the - sign in this case instead of either side of the = sign.
You could potentially do this for addition as well, now that I think of it, I frequently do.
11 + 14 + 22 is the same as 11 + 20 + 22 - 6. Along the way I gave it an extra 6 units to make the working process easier, then subtracted them at the end 53 - 6 = 47.
Multiplication in your head - the three major times-tables.
This is where things start to get much more interesting. Of all the people I know personally that are particularly smart, they all seem to use the same basic principles when working out multiplication. Many of them had the same trouble remembering the answers to their times tables as I did.
What does differ between each of them though, are particular habits and trends. It all works under the one big underlying principle of changing the presentation of the question, but the specific method ones uses is rather personal.
The whole idea of multiplication sits largely around the 10-times table and the 2-times table. You shouldn't need (though it is useful) to memorize a single answer either. The 10-times table is incredibly easy. When you times something by 10 you simply add a 0 to the end of the number. 10 x 10 = 100 or 10 x 23,456 = 234,560
The 2-times table is also incredibly easy. It's a case of doubling and nothing more (halving for dividing). 2 x 3 = 6 or 2 x 2364 = 4600 + 64 x 2 = 4728
From these two together, we can derive the final times-table required for a true understanding of quick mental multiplication. The 5-times table. This is also incredibly easy because it is the result of the ten times table halved (so really it's dividing by 2 not multiplying, but if you understand doubling then you undoubtedly understand halving).
So 5 x 45 is the same as (10 x 45) / 2
= 450 / 2
= 225
5 x 45 could also be worked out by adding 5 to the 45 and doing 5 x 50 = 250. Then you need to remember that you added 5 onto it so you have to remove 5 x 5 from this answer to get the answer to 5 x 45. So the final answer is 250 - 25 = 225.
In either case, only the 10x tables, 2x tables, addition and subtraction are used. This works because every multiplication is a part of two times-tables (except those that multiply by themselves ie 7x7). 2 x 3 belongs to both the 2-times table and the 3-times table. 7 x 8 belongs to the 7-times table and the 8-times table. When you cut it up, you are left with two chunks that are related to two of our three desired master-tables.
Even for 8 x 8, you can change it to 10 x 8 - 2 x 8 or 5 x 8 + 2 x 8 + 8. As long as you can reach a string of sums related to the master tables followed by any required addition or subtraction, you are going to have a walk in the park and plenty of bread to feed the ducks.

In the picture to the right I have approached the problem of 7x7 how I would normally. I have cut it up into two sums from the 5 and 2 times table that can be completed separately and summed together to gain the final answer.

Above is a diagram which shows how this process works using 47 grouped dots. Grouping objects to represent the numbers you are multiplying is an excellent way of demonstrating how and why the question can seem to become so mutilated and still reach the correct answer.


This understanding of multiplication becomes incredibly handy when you start to use it for anything outside of the 144 answers they force you to remember in school. Before deciding to write this article, I went around asking people I knew and people I met what 7 x 13 was. Very few of them even attempted it, and many of those who did struggled. The ones who did get the right answer, mostly reached their goal very fast. Using similar methods as I am here. Furthermore, they could tell you how they got the answer and every step along the way.
I wont go into explaining the examples to the right. If you are still reading then they should be pretty self explanatory by now. However, it does show how if you don't happen to remember a result of the 3 or 7 times table, you can still get the answer by breaking it down to the 2x, 1x, 10x or 5x tables. This will always be possible to do.


Here is a slightly harder example. All you have to do is take it one multiplication at a time. Start with 10 x 13 break it down until it's easy and take not of the answer. Then multiply your answer by 7, breaking it down until you can easily find your final answer. Please note that in the picture there is a typo. 10(10x3) should be 10(10+3). 10(10x3) is the same as 10 x 10 x 3 which would = 300. 10(10+3) is the same as 10 x 13.
In school you would be taught to "expand" 10(10+3) and you would know (because this is what they generally teach) that you have to multiply the 10 outside by the first 10 in the () and then by the 3 inside, which = 100 + 30. 100 + 30 gives you the same answer as 10 x 13. It's 130. This is what we are doing when we break things down in our minds. We are expanding in a similar fashion.
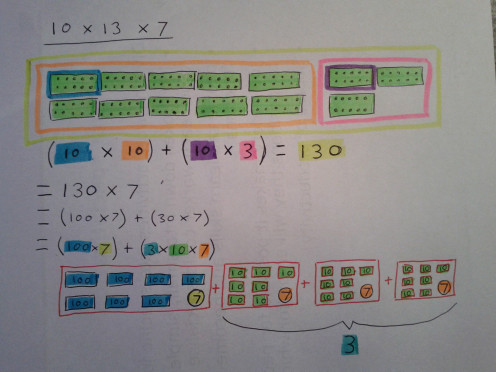
Ok so I know what you are thinking now. What in the world is this. It's mental. Well that's why I have colour-coded it for you. The colours in the top half of the picture correspond with each other independently of the bottom half and vice versa. If you are following the math though, it shouldn't be too hard to stay on track. All I'm trying to do is provide a graphical explanation as I did previously.

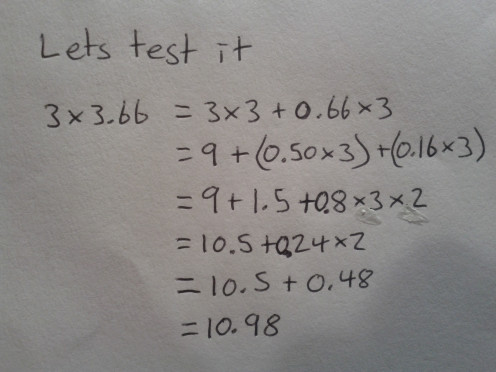
Division in your head
Division is a little more difficult. I think so at least anyway so if you have any tips, I'm all ears. What you need to remember is that it is multiplication, in reverse. Just like subtraction is addition in reverse.
It helps to know that 3 goes into 9 three times, but if you don't know then you can take some time to multiply 3 by another number in increments until you reach something close to 11. If I wanted to divide 123 by 16, this is how I would do it in my head.
16 x 2 = 32 (2)<-----how many times we have multiplied 16 aka the answer divided by 16
32 x 2 = 64 (4)
64 x 2 = 128 (8)
128 - 16 = 112 (7)
123 / 16 = 112 + 11/16
10% of 16 is 1.6 and 1% is 0.16
11 / 1.6
1.6 x 2 = 3.2
etc5
1.6 x 7 = 11.2 (because we already found 16 x 6 = 112, we can just shift the decimal point one place to the left) Therefore 11.2/16 = 0.70
11.2 - 0.16 = 11.04
So 11/16 is just under 0.69
So our final answer is approximately 7 + 0.69 = 7.69
With a calculator the answer is 7.6875
Pretty close hey! The only problem with this method is that it can be a bit slow and requires a fair bit of memory and concentration. Large divisions (because the smaller the number you divide by, the larger the slices of pizza you get) like 11 / 3 are quite easy though.

In the diagram, assume that all the black circles are identical pizzas. The ones that aren't entirely filled represent 2/3 of a Pizza. So dividing 11 Pizzas between 3 people; is the same as putting 11 circles into groups of 3.66
Furthermore, if you took away 2/3 of a pizza from one person and gave half of each to two other people: there would be two groups of 4 and one group of 3. This = 11. The diagram also shows the relationship between 9 divided by 3 and 11 divided by 3.
You can't divide 11 pizzas between 3 people without slicing them, so you share out 9 pizzas between 3 people and then share out the remaining 2 pizzas.
so we have turned 11/3 into 9/3 + 2/3 which is 3 + 0.66 = 3.66
I bet they didn't teach you that in school.....
Applying all of it together
The following is a large example which requires all the concepts throughout the article to figure out easily (easy is a relative word).
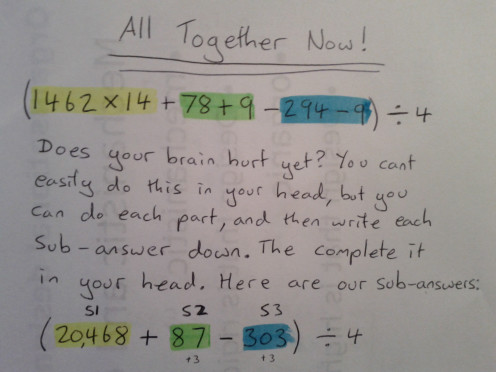
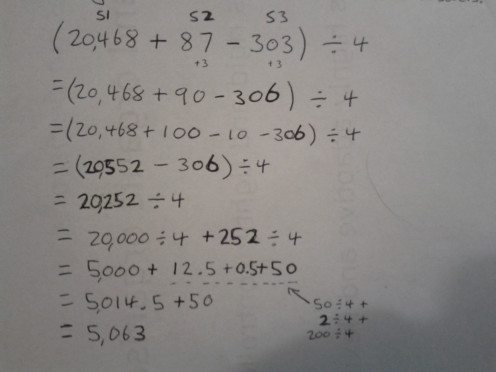
The secret to doing calculations in your head
Below I have tried to graphically provide an explanation of what goes on in my mind. You might get it you might not. It's not particularly important. What I have left out is that each green sub-answer should be added to the next before moving onto another. This way you don't have to remember all the sub-answers while you figure out all the sub-calculations. You only have to remember one at a time, cause each time you get a second you turn it back into one.
So for this particular question you only have to remember a maximum of 5 numbers at any one time. The numbers are 1462, 14 (from our question), one sub calculation (two more numbers here) and one sub answer. When you get a new sub answer you can forget it's sub-calculation so you are only remembering 4 numbers, then 3 when you add it to your previous sub-answer, then you have to remember 5 numbers again when you create the next sub-calculation to do.
You have to expand and reduce repeatedly in stages to reduce the number of things you have to remember at any one time. This is the secret to doing things in your head.
That's all I have to give for now. Please feel free to add anything related to the comments below or ask questions; and don't forget to practice! The more you refuse to use a calculator, the better you will get. Good luck!