Kruskal algorithm implementation in C
Kruskal Algorithm
Kruskal Algorithm
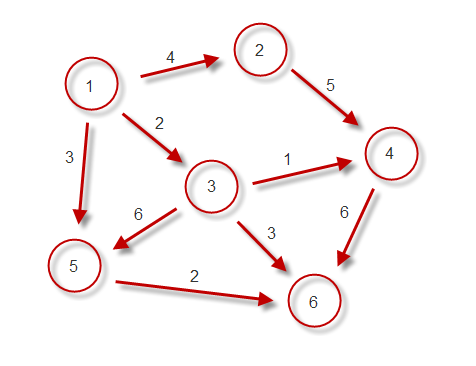
Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component). Kruskal's algorithm is an example of a greedy algorithm.
- create a forest F (a set of trees), where each vertex in the graph is a separate tree
- create a set S containing all the edges in the graph
- while Sis nonemptyand F is not yet spanning
- remove an edge with minimum weight from S
- if that edge connects two different trees, then add it to the forest, combining two trees into a single tree
- otherwise discard that edge.
At the termination of the algorithm, the forest has only one component and forms a minimum spanning tree of the graph.
C source code
#include<stdio.h>
#include<stdlib.h>
void printArray(int a[][100],int n);
void AdjacencyMatrix(int a[][100], int n){
int i,j;
for(i = 0;i < n; i++)
{
for(j = 0;j < i; j++)
{
a[i][j] = a[j][i]= rand()%50;
if( a[i][j]>40)a[i][j]=a[j][i]=999;
}
a[i][i] = 999;
}
printArray(a,n);
}
void printArray(int a[][100],int n){
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
printf("%d\t",a[i][j]);
}
printf("\n");
}
}
int root(int v,int p[]){
while(p[v] != v)
{v = p[v];}
return v;
}
void union_ij(int i,int j,int p[]){
if(j > i)
p[j] = i;
else
p[i] = j;
}
void kruskal(int a[][100],int n){
int count, i, p[100], min, j, u, v, k, t[100][100], sum;
count = k = sum = 0;
for(i = 0; i < n; i++)
{
p[i] = i;
}
while(count < n)
{
min = 999;
for(i = 0; i < n; i++)
{
for(j = 0;j < n; j++)
{
if(a[i][j] < min)
{
min = a[i][j];
u = i;
v = j;
}
}
}
if(min != 999)
{
i = root(u, p);
j = root(v, p);
if (i != j)
{
t[k][0] = u;
t[k][1] = v;
k++;
sum += min;
union_ij(i,j,p);
}
a[u][v] = a[v][u] = 999;
}count +=1;
}
if(count != n)
{
printf("spanning tree not exist\n");
}
if(count == n)
{
printf("Adges Spanning tree is\n");
for(k = 0; k < n-1 ; k++)
{
printf(" %d -> %d ",t[k][0],t[k][1]);
}
printf("\ncost = %d \n",sum);
}
}
int main()
{
int a[100][100],n;
printf("enter the number of vertices\n");
scanf("%d",&n);
AdjacencyMatrix(a,n);
kruskal(a,n);
return 0;
}
Content of Makefile
a.out: kruskal.c gcc kruskal.c PHONY:clean clean: rm *~ a.out