Mohammed ibn Musa al-Khowarizmi
Mohammed ibn Musa al-Khowarizmi, usually referred to simply as Al-Khowarizmi, was born in the town of Kheva in the region of Khwarezm, formerly part of Persia and now part of Uzbekistan, in approximately 770 AD. He was also an astronomer and geographer, allegedly credited with making the first globe of the known world, but he is most highly regarded as a very influential mathematician.
The Caliph, al-Mamun (809 -833), established a centre of learning at Baghdad, which was known as Bait al-hikma (House of Wisdom) and which was comparable to the ancient Museum at Alexandria. The Caliph had several of the famous Greek works, such as Euclid’s Elements and Ptolemy’s Almagest translated into Arabic.
Al-Khowarizmi was one of the faculty members at Bait al-hikma. He wrote more than a dozen works on mathematics and astronomy, influenced by Indian mathematicians such as Brahmagupta. These works included astronomical tables and treatises on the sundial and the astrolabe, but Al-Khowarizmi’s most famous works were two books on arithmetic and algebra. One of these works, known only by its Latin translation as De numero indorum (Concerning the Hindu art of reckoning) gives an account of Hindu numerals. Through this work, Al-Khowarizmi’s name became associated in Europe with the Hindu numerals, even though he made no claim to any originality in connection with the system; and an adaptation of his name has given us the word ‘algorithm’.
His other major work (written in approximately 820 AD) was a systematic study of the solution of linear and quadratic equations known as Hisab al-jabr w'al muqabalah (Calculation by restoration and the process of simplification). This work has become even more famous because our word algebra has been derived from al-jabr.
It is likely that Al-Khowarizmi was not familiar with the works of Diophantus such as Arithmetica , since he did not employ the use of syncopated algebra. On the contrary, Al-Khowarizmi used no symbols of any kind. He used words for everything, even numbers. On the other hand, Al-Khowarizmi’s work far surpassed that of Diophantus and the Hindu mathematicians who had influenced him; to the extent that he is often referred to as ‘The father of algebra’. The book Hisab al-jabr w'al muqabalah contains clearly explained methods to solve equations of the first and second degree – linear and quadratic equations. It consists of six chapters detailing the solution of six types of equation – in modern notation these were made up of terms in x2, terms in x and number terms.
According to Boyer (A History of Mathematics, Wiley 1968):
Chapter 1 deals with equations of the type x2 = 5x and x2/3 = 4x.
Chapter 2 deals with equations of the type x2 = 4 and x2/3 = 12
Chapter 3 deals with equations of the type 3x = 15
Chapter 4 deals with equations of the type x2 + 10x = 39
Chapter 5 deals with equations of the type x2 + 21 = 10x
Chapter 6 deals with equations of the type 3x + 4 = x2
Note that Al-Khowarizmi gave only positive roots, and ignored negative and zero roots.
For example:
His solution for x2 = 5x was x = 5. He did not give the other solution x = 0
His solution for 3x + 4 = x2 was x = 4. He did not give the other solution x = -1
But he gave both solutions, x = 3 and x = 7, for x2 + 21 = 10x
Al-Khowarizmi died around 850 AD.
A contribution of Al-Khowarizmi to mathematics
To justify his solution of an equation such as x2 + 10x = 39, Al-Khowarizmi also gave geometrical proofs.
Consider this example x2 + 10x = 39 (1)
Construct a square ABCD with sides (x + 5) as follows:
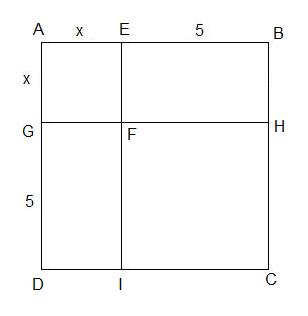
In this case:
The area of square AEFG = x × x = x2
The area of rectangle EBHF = 5 × x = 5x
The area of rectangle GFID = 5 × x = 5x
Therefore Area of square AEFG + Area of rectangle EBHF + Area of rectangle GFID
= x2 + 5x + 5x
= x2 + 10x
But this is the same as the left hand side of equation (1), and therefore equals 39
Therefore Area of square AEFG + Area of rectangle EBHF + Area of rectangle GFID = 39
Now add the area of square FHCI = 5 × 5 = 25
Therefore Area of square AEFG + Area of rectangle EBHF + Area of rectangle GFID + Area of square FHCI = 39 + 25 = 64
Therefore Area of square ABCD = 64
Therefore (x + 5)2 = 64
Therefore x + 5 = √64 = 8
Therefore x = 8 – 5 = 3
Note:
1. I have shown this proof using modern notation. Al-Khowarizmi did it using only words.
2. Only the positive value of x is given. Modern algebra tells us that -8 – 5 = -13 is another solution.