Maths help: Algebra - how do you simplify algebraic expressions? How do you add algebraic expressions?
An example of Algebra
Many people who come to learn about algebra are familiar in seeing missing number equations:

If you look above, then most people will know the answer is 18.
The missing number within that number sentence to make it accurate must be 18 because 1 + 18 = 19. A lot of children seeing this know this without much help. The maths behind it is to work with inverses. 19 -1 = 18.
Simple algebra just replaces this missing number with a letter.
1 + a = 19, so a = 18 because of the same reasons above.
What is algebra?
Algebra has a bad reputation. Ask your mother or father about it and you might see a slight shudder from them when they think of their school days dealing with this difficult concept.
When you stop trying to think of maths as having a definative answer it gets easier. Algebra exists because sometimes there just isn't that definative answer we seek. It is all about finding the unknown or putting real life problems into equations and then solving them.
The hard thing is seeing that it really does relate to real life. Maths is related to real life! Are you joking I hear you say. Well, yes, maths is used in every day life more than you think.
Algebra is a branch of maths that substitutes letters for numbers. It is where an algebraic equation represents a scale, where the 'answer' can change depending on what number you substitute back into the equation.
Why do we need Algebra?
Algebra is a great way to develpop great life skills like thinking logically, problem solving, deductive and inductive skills as well as spotting patterns and of course you can't go onto studying or working with higher order maths without it.
Jobs in engineering, physics or any other scientifical job, computer programming and acountants all need algebra within their jobs. But of course, maths is seen as a great way into college or university.
How do you simplify algebraic equations?
Start to think about algebra like this:
2 Banannas + 3 Apples.
If I was going to write this out as an algebraic number sentence I would write:
2 B + 3 A
When you add look at this, it is important that you can't add banannas and apples. If you did try you would still have 2 banannas and 3 apples, so you couldn't simplify it at all. With this in mind it is the same with algebra - you can't add a B to an A. 2B + 3A is still 2B + 3A.
If you can't add different letters how do you simplify?
Simplifying is trying to make the equation as easy as possible. Simplification can occur when you can add or take different parts of the equation like this:
2 Banannas + 3 Apples + 1 Bananna = 3 Banannas + 3 Apples.
This is possible because we can add the banannas up to make 3 banannas to simplify it.
This wrote as an algebraic equation would look like this:
2B + 3A + 1B = 3B + 3A
Again this is possible because we can add up the B's to make 3B. This makes it simpier and easier to work out the answer.
Algebra - when simpifying just collect the like terms
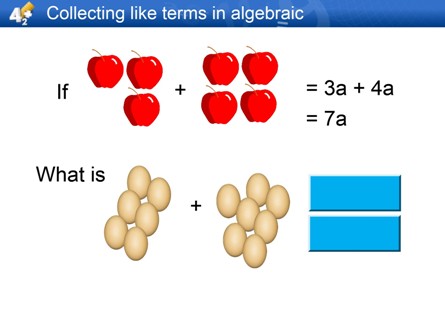
- In the above picture we start off with 3 apples and 4 apples. This is easily added together to make 7 apples.
If we change this to algebra we get 3A + 4A = 7A
- In the next example we have 6 eggs and 7 eggs. So if we added these up we get 13 eggs.
If we changed this to algebra too, then we get 6E + 7E = 13E
- There is no way we can add apples and eggs like we can't add A and E in algebra.
Example 1:

If we wrote that number sentence, then we would get:
3 Banannas + 2 Apples + 2 Banannas = 5 Banannas + 2 Apples
Algebra is exactly the same as this when we simplify the number sentence:
If we wrote that in algebraic form:
3B + 2A + 2B = (3B + 2B) + 2A = 5B + 2B
You take the like elements; in this case the B's (banannas) and then add them up.
Example 2:

The caption above says it all - collect like terms.
So with the example of 4a + 5 + 2a - 3
The 4a and the 2a can be added. Think of them as 4 apples and 2 apples, which make 6 apples. So 4a + 2a = 6a.
Then there are a few numbers in this example too, which we can all work out. So collect them together, 5 and -3. The number sentence to work out here would be 5-3 =2.
So 4a +5 + 2a -3 = (4a + 2a) + (5-3) = 6a +2
Remember to work out what is in the brackets first.
Example 3:
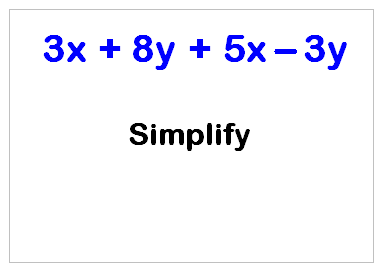
The example above is a little more complicated as it has lots of terms:
But don't worry, just follow the same rule - collect the like terms.
3X + 8Y + 5X -3Y = (3X + 5X) + (8Y - 3Y) = 8X + 5Y
Collect all the X's together and then work out what you have left. Then collect the Y's together and then work out what you have left there too.
Have a go at some questions:
view quiz statisticsHave a go at this website to practice what you have learnt here.
- Play Add and subtract terms with multiple letters. A fun Algebra maths game about Simplifying algebr
Add and subtract terms with multiple letters, Algebra Maths Games - From Mangahigh.com