Multiplying and Dividing Exponents. What are the rules for multiplying and dividing powers?

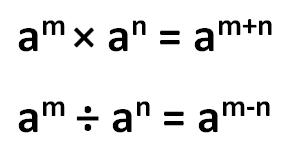
The quick rules for multiplying and dividing exponent that have the same base numbers are as follows:

a^m×aⁿ = a^m+n (so you just need to add the exponents)

a^m ÷aⁿ = a^m-n(so take the second exponent from the first)

So basically, add the exponents for multiplying and work out the difference for dividing.

Example 1

Simplify x⁷ × x^⁴

Since you are multiplying add the exponents:

x⁷ × x^⁴ = x⁷⁺⁴ = x¹¹

Example 2

Simplify y⁸ × y

Again you are multiplying the exponents so add them together. Also y has an exponent of 1:

y⁸ × y = y⁸⁺¹ = y⁹

Example 3

Simplify x¹² ÷ x⁹

This time you are dividing the terms so work out the difference:

x¹² ÷ x⁹ = x^12-9 = x³

Example 4

Simplify a⁵/a⁷

This time you are dividing the terms so work out the difference again:

a⁵/a⁷= a^5-7 = a^-2

Example 5

Simplify x⁶y² × x⁴y¹⁰.

Here, you need to add the exponents of the x terms and add the exponents of the y terms:

x⁶ × x^⁴ = x¹⁰

y² × y¹⁰ = y¹²

So if you put these together you get a final answer of:

x¹⁰ y¹²

Example 6

Simplify x⁸y⁷ ÷ x⁴y³.

Here, you need to take the exponents of the x terms and also take the exponents of the y terms as you are dividing:

x⁸ ÷ x⁴ = x^8-4 = x⁴

Y⁷ ÷ y³ = y⁴

So if you put these together you get a final answer of:

x⁴ y⁴

Example 7

Simplify 7c⁶d⁸e⁴ × 8c³de^-9

This is not as hard as it looks.

First multiply 7 by 8 to give 56 (don’t add these together as they are not exponents). This will go at the start of your answer.

Next work out the exponents of c, d and e by adding the exponents as it’s a multiplication:

c⁶×c³ = c⁹

d⁸×d¹ = d⁹

e⁴×e^-9 = e^-5

So if you put all of these answers together you get the expression:

56c⁹d⁹e^-5

So to summarise, multiplying exponents you add the powers and dividing exponents take the powers.