Names of Different Types of Angles
By Joan Whetzel
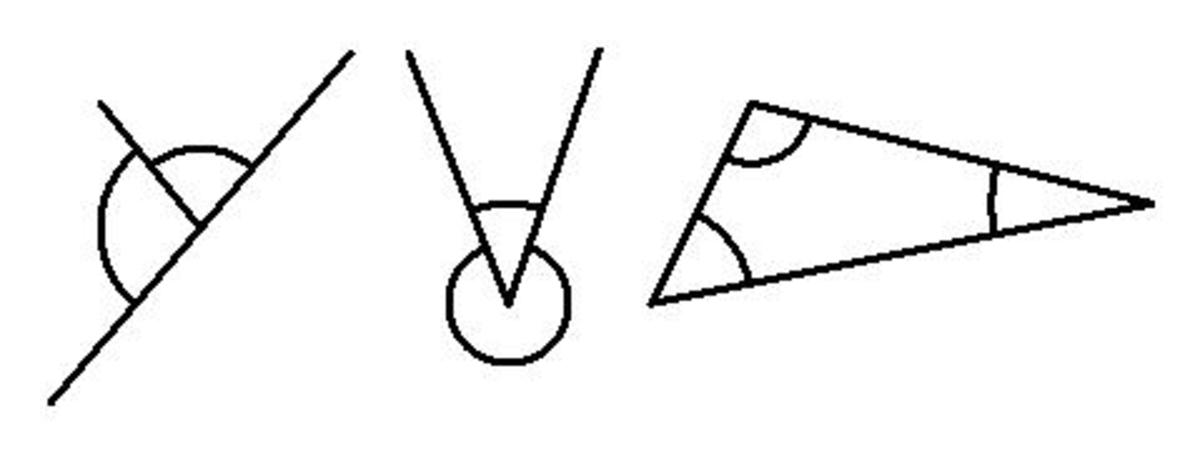
Angles are a primary unit in the study of Geometry. Angle sizes are measured in degrees of the circumference of a circle. Full circles are 360 degrees. A half circle and straight line have 180 degrees. Cutting that circle into quarters, gives a right angle that measures 90 degrees. There are several types of angles each with its own proportions which are measured in degrees. Basically, an angle is defined as two lines along a plane, which meet or intersect at a juncture point, called the vertex . The lines are not straight with respect to each other, with the exception of the straight angle, which measures 180 degrees. These various angles are used to design buildings, roads, artwork of all kinds, and furniture. The names of the different types of angles are:
- · the acute angle
- · the right angle
- · the obtuse angle
- · the straight angle
- · the reflex angle
- · the complimentary angle
- · the supplementary angle
- · the vertical angles
- · the congruent angles
Acute Angles
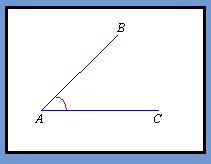
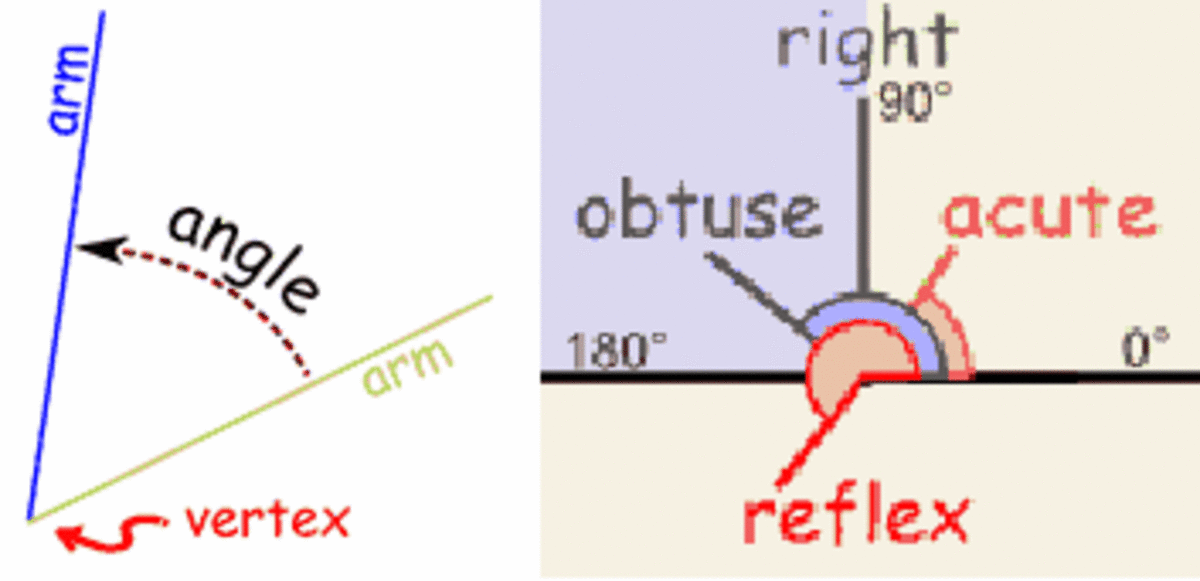
Acute angles are any angle that measures less than 90 degrees but greater than 0 degrees. The equation for this is: 0 < theta < 90. Acute angle examples include: 20 degrees, 45 degrees (1/8 of a pie), 75 degrees, and 89 degrees.
Right Angles
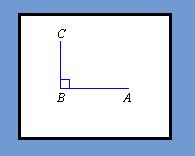
Right angles equal exactly 90 degrees, meaning the lines run perpendicular to each other. If the open end of the angle is closed in by an arc, it would look like a quarter of a circle or a quarter of a pie.
Obtuse Angles

Obtuse angles have measurements less than 180 degrees and greater than 90 degrees. That would make these angles look like something between a quarter of a pie and a half of a pie. The equation would look like 90 < theta < 180. Obtuse angles run anywhere from 91 degrees to 179 degrees.
Reflex Angle
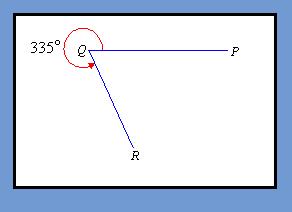
Reflex angles are greater than half of a circle or pie, but not quite the whole pie. Reflex circles are less than 360 degrees but greater than 180 degrees .
Straight Angle
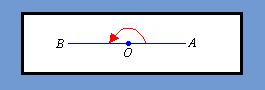
Straight angles are the easiest to draw since they are, in essence a straight line with vertex at the center. Straight angles measure exactly 180 degrees and, if closed in by an arc by the two outer points, would form a half circle or half a pie.
Complimentary Angles
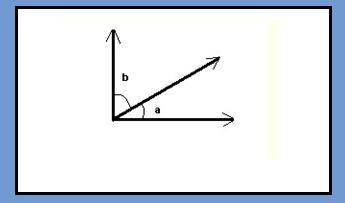
When two acute angles are joined together so that they share a common vertex, and the combined angles measure 90 degrees, then a complimentary angle has been formed. It would be like cutting two slices of pie, then placing them together on a plate so that they look like a quarter of the pie has been removed. The two angles, or pie slices, do not have to have the same measurements, They only have to equal 90 degrees when joined together.
Supplementary Angeles
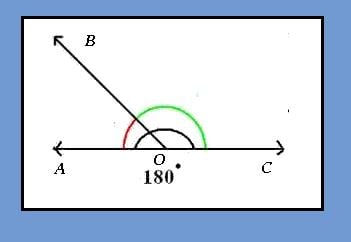
When an acute angle (less than 90 degrees) and an obtuse angle (less than 180 degrees but more than 90 degrees) are joined together so that they share a common vertex, and equal exactly 180 degrees, then a supplementary angle has been formed. Like the complementary angle, it's like putting two pieces of pie of different sizes on a plate so that they form half the pie.
Vertical Angles
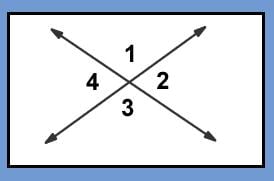
Vertical angles are formed when two lines intersect each other so that there are 4 angles with a common vertex. All four angles put together will form a full circle and add up to 360 degrees. The angles may all be acute angles or they may be two sets of supplementary angles meaning two of the angles (angles 2 and 4 in the above picture) will be smaller and have the same measurement in degrees, and the other two angles (angles 1 and 3 in the above picture) will be larger with the same measurement in degrees.
Congruent Angles
Two angles are congruent when they have the same measurement. In the picture of the vertical angles above, angles 1 and 3 are congruent and angles 2 and 4 are congruent. An equilateral triangle will have 3 congruent angles. A polygon (pentagon, hexagon, octagon) will also have congruent angles.
References
Maths Teacher: Year 7 Interactive Maths - Second Edition, Angles
http://www.mathsteacher.com.au/year7/ch08_angles/01_ang/ang.htm
Utah Education Network: Angles, Degrees, Protractors…Oh My!
http://www.uen.org/Lessonplan/preview.cgi?LPid=21520
Tutor Vista. Angles.
http://www.tutorvista.com/search/angles
Math Open Reference: Degrees
http://www.mathopenref.com/degrees.html
Math Is Fun: 45 Degree Angle
http://www.mathsisfun.com/geometry/construct-45degree.html
Hot Math: Degree Measure of an Angle
http://hotmath.com/hotmath_help/topics/degree-measure-of-an-angle.html
Free Math Help: Interior Angles of a Polygon
http://www.freemathhelp.com/feliz-interior-polygon.html
Wikipedia. Angle.