Fractional Exponent Law. How to work out the value of fraction exponents.
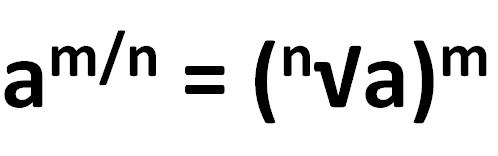
A fractional exponent can be worked out by applying the following rule:
am/n = (n√a)m
This means the nth root of a raised to the power of m. This is easier to see if you take a look at some numerical examples:
Example 1
Work out the value of 163/2.
All you need to do is apply the above rule for working out negative exponents:
163/2 = (2√16)3
So first work out what’s inside the bracket, that is, the square root of 16 (2√16 is the same as √16):
(2√16)3 = 43 (since the square root of 16 is 4)
Next work out the cube of 4 to give the final answer:
43 = 64 (since 4 × 4 × 4 = 64)
Example 2
Work out the value of 811/2.
Again, all you need to do is apply the above rule for working out negative exponents:
811/2 = (2√81)1
So first work out what’s inside the bracket, that is, the square root of 81 (2√81 is the same as √81):
(2√81)1 = 91 (since the square root of 81 is 9)
Next work out the 9 to the power of 1 to give the final answer:
91 = 9
Example 3
Work out the value of 82/3.
Again, all you need to do is apply the above rule for working out negative exponents:
82/3 = (3√8)2
So first work out what’s inside the bracket, that is, the cube root of 8:
(3√8)2 = 22 (since the cube root of 8 is 2)
Next work out the square of 2:
22 = 4 (since 2× 2 = 4)
Example 4
Work out the value of (64/125)1/3.
First of all (64/125)1/3 can be written as 641/3/1251/3
Next, apply the negative exponent rule separately to the numerator and denominator of the fraction you have just made:
641/3= (3√64)1
1251/3 = (3√125)1
So all you need to do now is work out the cube root of both numbers:
(3√64)1 = 4
(3√125)1 = 5
So the final answer to (64/125)1/3 = 4/5