Pythagoras proof. An easy to understand proof of Pythagoras Theorem a^2 + b^2 = c^2
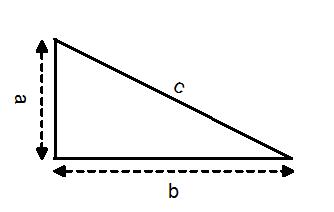
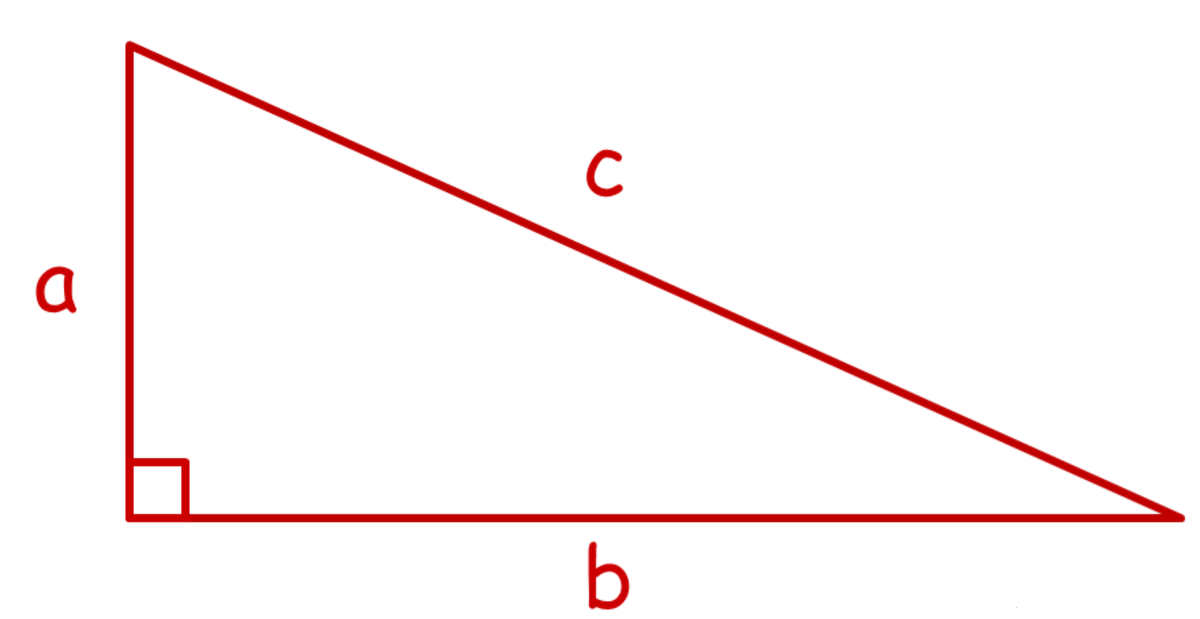
In this hub I will show you a simple proof of Pythagoras Theorem, that is, the square of the hypotenuse of a right angled triangle is equal to the sum of the squares of the other two sides:
a² + b² = c².
The proof can be done by fitting 4 congruent right angled triangles together to make a square and writing the area of the square down in 2 different ways. This is probably one of the easier and nicer proofs of Pythagoras.
First start off with a right angled triangle and call the sides a,b and c (c being the hypotenuse).
Next you will need to draw another 3 congruent triangles to this first right angled triangle by rotating it through 90⁰, 180⁰ and 270⁰ clockwise.
Fit these 4 triangles together to make a square of side length a + b. You will also notice that there is a square of side length c made inside the larger square.
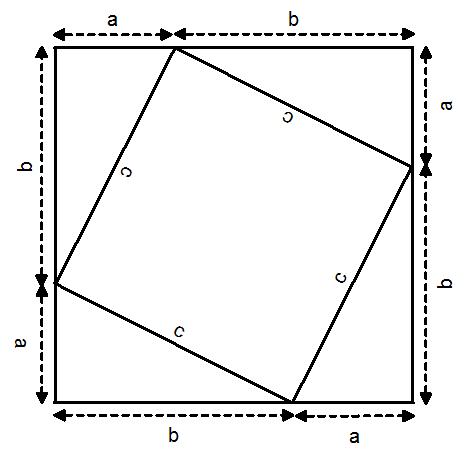
Now the area of the large square has an area of (a+b)(a+b). If you expand and simplify these double brackets you get A = a² + 2ab + b². Call this formula 1.
You can also make another formula for the area of the large square by summing the area of the four triangles and the smaller square inside the large square:
4 × ½ × a × b + c × c
So A = 2ab + c²
Call this formula 2.
So the two formulas that we have made for the area of the large square are:
A = a² + 2ab + b² and A = 2ab + c².
All you need to do is equate both formulas as both formulas made give the area of the large square:
a² + 2ab + b² = 2ab + c².
If you notice there is a 2ab term on both sides of the equation. All you need to do now is subtract 2ab from both sides. This will give you the required result:
a² + b² = c²