Pythagorean Trigonometry a quick proof

[Sin(x)]^2+[Cos(x)]^2=1. This is one of the first proofs that we learn in trigonometry. It is based on the pythagorean formula.

Okay lets have a few definitions:

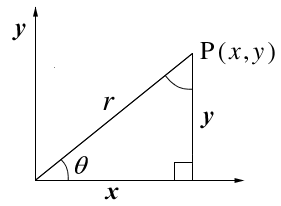
On a right triangle:

Sin(x)=opposite leg/hypotenuse or =opp/hyp
Cos(x)=adjacent/hypotenuse or =adj/hyp

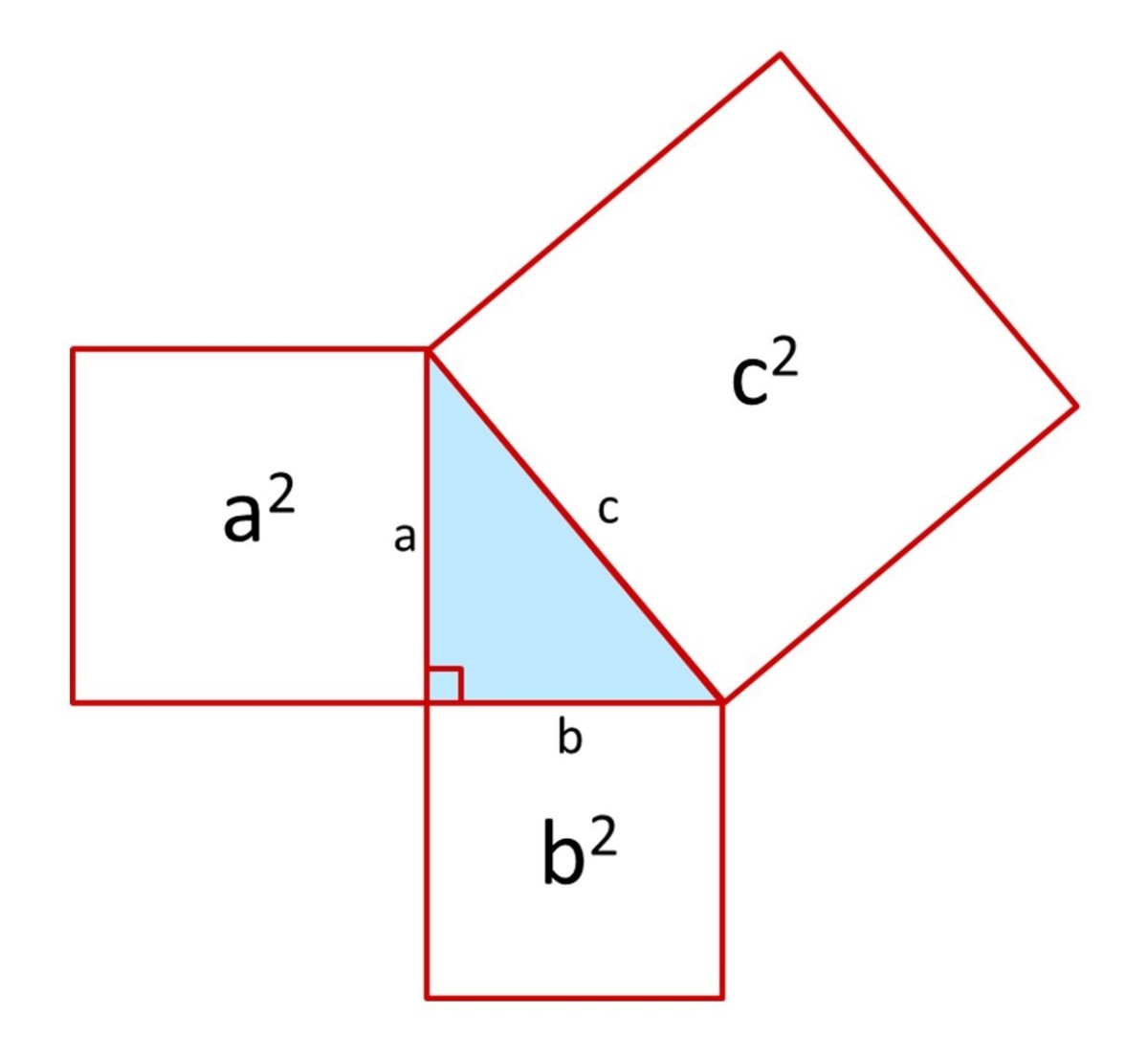
The pythagorean theorem (on the same triangle)

(opp)^2 + (adj)^2=(hyp)^2

Everything is defined so lets divide both sides of the pythagorean equation by (hyp)^2. We now have:

(opp)^2/(hyp)^2 + (adj)^2/(hyp)^2= 1

Again we know that Sin(x)=opp/hyp and Cos(x)=adj/hyp.

Therfore: [Sin(x)]^2+[Cos(x)]^2=1

We can also do this with other trignometric functions. Lets look at tan(x) and sec(x)

tan(x)=opp/adj and sec(x)=hyp/opp

Back again to the pythagorean formula but we are going to change it a little bit:

adj^2=hyp^2 -opp^2 (This can be done by subtracting opp^2 from both sides)

Lets divide both sides of the pythagorean formula by adj^2 and we have:

1=hyp^2/adj^2-opp^2/adj^2

Now remember: tan(x)=opp/adj and sec(x)=hyp/opp so:

1=[sec(x)]^2-[tan(x)]^2 or [tan(x)]^2 + 1=[sec(x)]^2

Can you do the proof of this trigonometry identity:

[cot(x)]^2 +1=[csc(x)]^2?