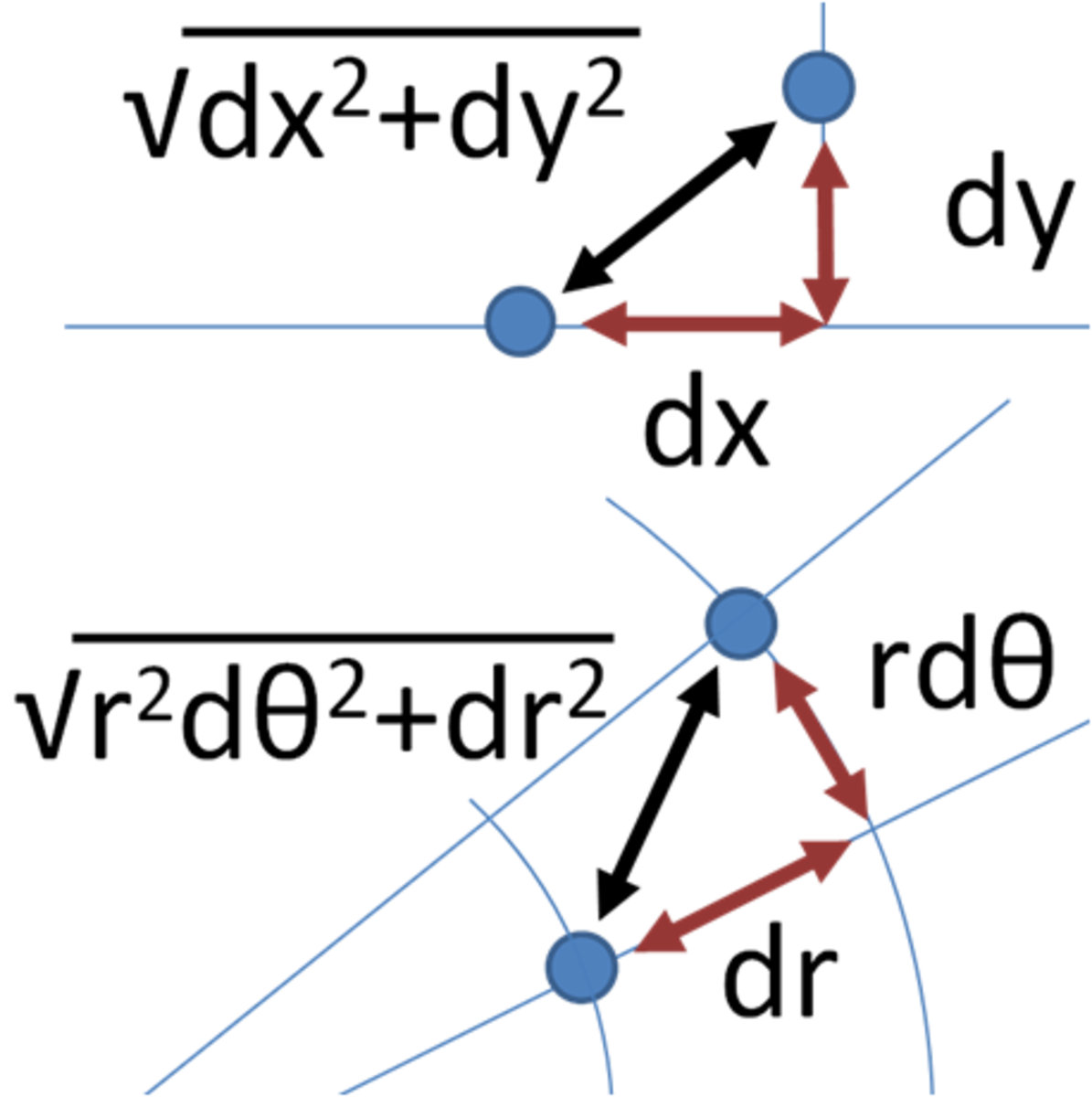
The Beginning of Mathematics: Invention of the Proof

Counting, Measurement, and Form
All human cultures have number words. Writing as a human invention may have had its origin in the action of record keeping. Ancient bone scratches for example indicate the earliest known form of arithmetic and accounting. The stars enabled ancient farmers to keep track of the seasons and allowed sailors to navigate so the study of the stars gave way to superstitions as well as astronomy. And with the rise of the cities, numbers took on a more exalted role. Architects attempted to perfect proportion and symmetry, philosophers equipped with rulers and straight edges sought to understand the dimensions of the world. By the time of Ancient Greece, the time was right for mathematical progress. So, the question arises: at what point does number knowledge become mathematics?
The Mathematical Proof
There is one discovery that distinguishes mathematics from what I would term practical knowledge about counting, measurement: the mathematical proof.
The proof enabled a level of certainty regarding mathematics that was unprecedented. While it is very easy to make a mistake in a proof or to base a proof on questionable or contradictory premises, the proof is still one of the first important breaks from what would otherwise be a practice or a craft.
With the method of the proof, mathematics becomes a rational science consisting of postulates (premises), argument (proof), minor conclusions (lemmas) and major conclusions (theorems). With this idea, mathematics as the first science was born.

Thales
According to legend, the inventor of the mathematical proof was an eccentric genius named Thales who lived on the island of Ios. He would wander the world astounding people with his insights.
Using his technique of proof, he could make predictions that were held out in practice. His achievements are well chronicled by the ancients.
Did Thales really exist? It is hard to say but it is very nice that there is a name to associate with the beginning of mathematics.
According to legend, Thales provided proofs for the following theorems:
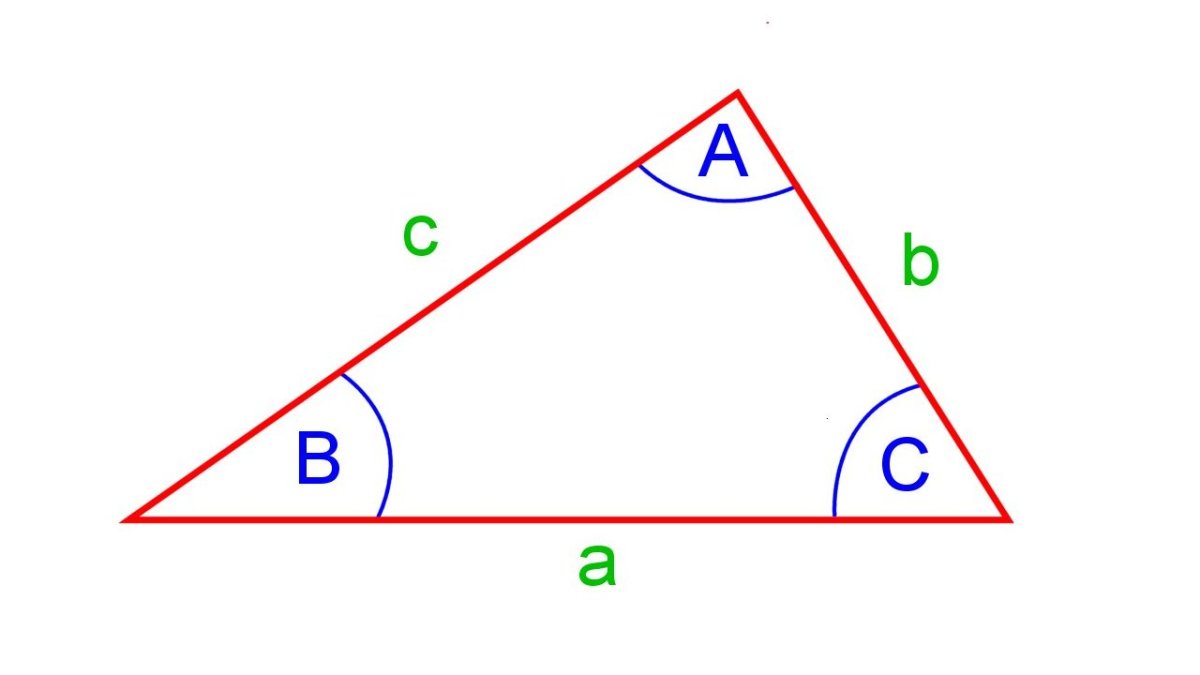
- A triangle with two equal sides also has two equal angles.
- If two triangles have two angles equal and one side equal, then all remaining sides and the remaining angle are also equal.
- If two lines intersect, then both of the two opposite angles formed at the intersection are equal.
- Any triangle formed between the two points on the diameter of a circle and a third point on the circumference of the circle will be a right triangle.