What is an Intersection of Two Sets?
Introduction
A set is zero or more items grouped arbitrarily. Typically a particular set contains items with some relationship outside the grouping, but that is not a requirement. We may use the word collection as well to describe such an accumulation of things.
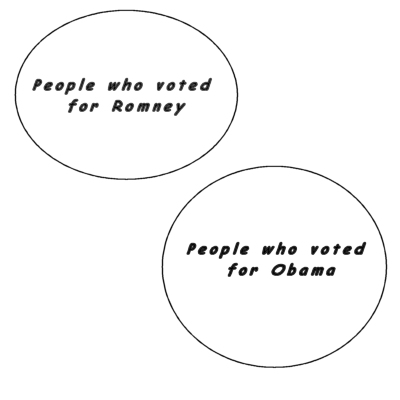
For example, all the people who voted in the 2012 United States Presidential Election for Barack Hussein Obama may be considered to be a set. This example is for conceptual purposes only: we cannot hope to identify the particular people belonging to the set nor would we be able to gather them all together into a manageable group.
A more tenable example would be all the spoons in your silverware drawer in your kitchen. This set is precise, countable, and small enough to be manageable. We are not going to debate the definition of 'spoon.'
Some set notation
When we describe the contents of a set, we use set notation. One style of such symbology uses curly brackets (also called curly braces) to delimit the beginning and end of the list of items in the set. We use commas to separate the individual items from each other.
For example:
{1,2,3,4}
is a set of 4 numbers.
We can also add non-numeric items to our set:
{1,2,3,4, "apple", "peach"}.
Delimiting individual set items with quotation marks is not necessary in the preceding example, but non-numeric items with embedded commas would become problematic. For example:
{1,2,3,4,apple,peach}
could be a set with either 5 or 6 items. The last item could be apple,peach or just peach. For this reason we endorse the use of quotes for all non-numeric list items whenever possible.
Referring to sets
In order to write simple expressions in any branch of mathematics, we create placeholders to represent our sets. Consider the set of fruits defined here:
{"banana", "grape", "plum", "strawberry", "tomato"}
instead of listing all the elements whenever we want to refer to the set, we can define a simple placeholder, or variable, to represent the entire set. This variable is usually a capital letter. We might write:
F = {"banana", "grape", "plum", "strawberry", "tomato"}.
Where the F is the variable. We chose F because the list contains fruits. You may choose your own letters to meet your own documentation requirements.
Sets have operations
Operations can be performed on sets. These operations are typically mathematical or logical but text-based operations are also possible. A small collection of operations common to all sets can be discussed.
- Count
- Enumerate
- Add
- Remove
We would want to perform these operations on almost any set. The particular content of the set doesn't matter: this collection of operations is general enough to apply almost all the time.
Sets that cannot be enumerated
Some sets are so large as to be impossible to enumerate. We can still define the contents of such a set in a qualitative manner rather than a quantitative notation. For example:
A = {All the people who have FaceBook accounts}
Obviously this set changes almost constantly, but conceptually we understand what it represents. The Letter A will be used as our variable to represent the set in equations and formulas.
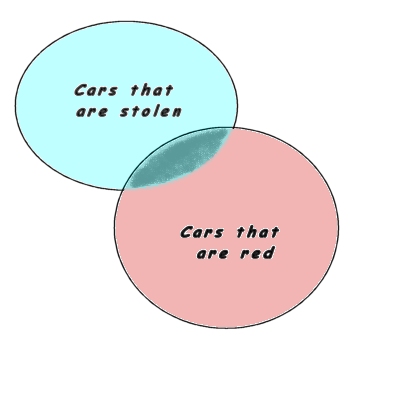
Intersection
Two sets intersect when each set has one or more items that are also in the other set. We use the ∩ symbol to represent the intersection operation on two sets.
For example:
A ∩ B
is the intersection of set A and set B. We don't know what is in sets A and B, but if we did we could calculate the intersection.
Here's a more practical example:
Y = {1,2,3,4}
X = {2,4,6,8}
The intersection of sets A and B can be written as X ∩ Y = {2,4}.
Here's another notation
Not all of us are numerically-minded. Many folks have an easier time visualizing diagrams or drawings rather than numbers and variables. To that end, a mathematician called John Venn devised a style of representing set intersections that is named after him to this day. The Venn Diagram can be used to illustrate the intersections of small sets of sets. Refer to the example below.
Limitations of the Venn Diagram
A typical Venn Diagram is drawn in two dimensions, therefore limiting its effectiveness for sets counts of any appreciable size. We can deploy Venn Diagrams to illustrate the intersection of two sets and sometimes three, but the illustration will become unwieldy and unclear rather quickly.
What if two sets do not intersect?
We can always write
A ∩ B
to illustrate the intention to calculate the intersection between sets A and B. However, there may not be any intersection: no items in A may be common to B. In that case, we use a special notation called the empty set to illustrate our non-intersection. We write:
A ∩ B = {}.
An empty set is described simply as an opening curly brace immediately followed by a closing curly brace. Any spaces or blanks enclosed within the braces are ignored, so we can write
A ∩ B = { }
without getting into trouble.