What is the radius of circle if the pink area equals the green one?
What is the radius of circle if the pink area equals the green one?
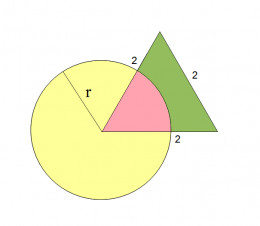
Because the triangle is equilateral, the angle for the pink area is 60 degrees, which is 1/6 of the 360 degree circle. So the area of the pink shaded region is pi * r^2 / 6.
The height of the triangle is sqrt (4 - 1) = sqrt (3). Which makes the area of the whole triangle= sqrt (3) * 2 / 2 = sqrt (3). So the area of the green shaded region = area of the whole triangle - area of the pink shaded region = sqrt (3) - pi * r^2 / 6.
Given that the area of the pink shaded region = area of the green region, we get the following equation:
pi * r^2 / 6 = sqrt (3) - pi * r^2 / 6
Solving for r:
pi * r^2 / 3 = sqrt (3)
r^2 = 3 * sqrt (3) / pi
r = sqrt [3 * sqrt (3) / pi]Since the area of the triangle is sq rt 3, then pi r^2/6 must equal (rad 3)/2. cross multiplying and dividing by 3 and simplifying gives approximately 1.654 = r^2 taking the sq rt of each side gives approximately 1.286.
Both solutions are correct! (so I select the first answer as the best) The area of triangle is sqrt(3), and than we use formula for the pink area: A=r^2 *pi * alpha /360, where the angle alpha is 60 (since we have equilateral triangle).
Related Discussions
- 9
Imagine a cake in the shape of an equilateral triangle as shown in the image bel
by Christopher Wanamaker 11 years ago
Imagine a cake in the shape of an equilateral triangle as shown in the image below. Each side of thetriangle cake measures exactly 8 inches. What is the length of the shortest possible cut that will divide the cake into two pieces with equal area?
- 3
what is the area of circle?
by ahmed.muhamad 13 years ago
what is the area of circle?
- 12
What is the area of pink triangle?
by flysky 11 years ago
What is the area of pink triangle?
- 34
Please Explain this Mathematicians
by Cindy Lawson 3 years ago
Okay, just heard this on a TV programme/documentary, but sadly missed the crucial solution. It is now bugging me no end, I just can't explain it, so I need someone, anyone in fact, to explain to me how this works. Here goes:3 friends go to a restaurant for a meal.The bill arrives and it is for...






