What are Integers?

Review of whole numbers
We call the set of natural numbers plus zero the set of whole numbers or W.
W= N + {0}
0 is called the identity under addition.
The set of whole numbers has all the properties of the natural numbers plus the properties of 0
Properties of Identity 0
a + 0 = a
First contact with negative numbers
A more difficult concept is the concept of “negative” numbers.
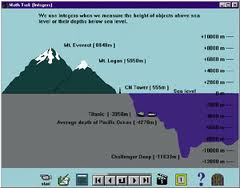
Negative numbers arise as follows: suppose you owe someone three dollars. If you receive three dollars, you will first have to pay back the money you owe. You will have no money left. You could say that you now have zero dollars. Or a diver is six feet underwater. The diver has to rise six feet before he is at ground level again.
How can we express mathematically the money we owe or the depth of the diver?
Debts, depths, sub zero temperatures are just a few of the situations which are represented by negative numbers.
Thus a debt of $3 is written $(-3).
The depth of 6 ft is written (-6)ft
We now can write:
$(-3) + $(+3) =$0. (-3) represents the money you owe.
(-6)ft + (+6)ft = 0ft . (-6) represents the depth of the diver. 0 represents ground level.
The set of integers
The set of Integers is the set of whole numbers plus the negative versions of the counting numbers.
Z = {…( -4), (-3),( -2), (-1), 0, 1, 2, 3, 4,…}.
We now notice that for every integer a there is another integer called (-a) such that: a + (-a) = 0.
(-a) is called the inverse of a under addition.
Thinking Questions: 1)what is the inverse under addition of 3? What is the inverse under addition of (-3)? 2) what is the inverse under addition of 0?
Integers have all the properties of the whole numbers plus the property that every number has an additive inverse.
We now no longer need the operation of subtraction. For any two integers m and n,
m-n = m + (-n) (where (-n) is simply the inverse under addition of n).
- Integers
The Integers are introduced. Integers are positive and negative whole numbers. Learn integers with lessons from Math Goodies.