A Bit of Musical Geekiness
There's a very good chance that if you know the Circle of Fifths well, you already know a lot about transposing music from one key to another. But it may also happen that you enjoy knowing some odd or peculiar facts that might at some point actually prove to be useful. One of these "facts" is that there are several ways to use the Circle of Fifths as an aid or a tool in transposing music.
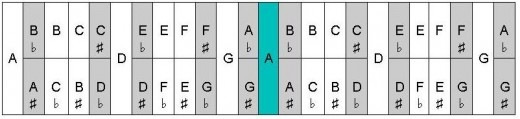
If you would like to try this bit of assistance, the first thing you need to do is to convert the interval (the distance you wish to transpose) to half-steps. If that does not happen naturally in your mind, use the "Musical Half-Steps" chart below. [Half-steps are also known as semi-tones.] It shows the notes of the music alphabet as if they were keys on a keyboard. The gray sections represent black keys, and most keys show alternative names for each note. This chart would be useful in a situation where you know that you wish to transpose, for instance, from D minor to Gb minor and you need to check yourself on how many half-steps that represents. Count the boxes following the D, moving to the right until you reach F#/Gb, and count that box ( = four half-steps, aka semi-tones). [You may also be aware that you can transpose down from D to Gb. That will be discussed somewhat, at a later point.]
Musical Half-Steps
Why Bother with This?
It is probably a good idea at this point to explain a bit about what this use of the Circle of Fifths can and cannot do.
In using the Circle as an aid to transposition, you should be able to see at a glance the names of the primary and secondary chords in the new key, corresponding to the primary and secondary chords in the original key. These important chords are clustered around the tonic, as explained in "New Uses for the Circle of Fifths." Not only does this show the names of the new chords in the new key, but the names of the notes themselves will correspond as well.
So, for example, the I chord of the original key (let's say G) will become the I chord of the new key (in this example Eb). And the ii chord (in G = Am) will become the ii chord in Eb (=Fm); the iii chord of G (Bm) will become the iii chord in Eb (Gm); the IV chord of G (C major) will become the IV chord of Eb (Ab major); G’s V chord (D major) will be transposed to Eb’s V (Bb major), and the vi chord of G (Em) will become the vi chord of Eb (Cm). The vii° diminished chord for each, not shown on the cluster of chords on the Circle, would be the transposed equivalent (F#° --> D°). Just remember that the seventh degree, in a major key, is a half-step below the tonic. In a minor key, the second degree is the one that is missing from the Circle's cluster of chords/notes, and it is the note that is a whole step higher than the tonic.
This tool can enable you to find notes if you are struggling, or to check yourself if you just need confirmation of the work you have done.
However, if you are talking about individual notes, the methods described here will not distinguish between the alternate names of the notes. You need to know the actual key and context of what you are transposing to decide whether to call a note Ab or G#.
"Always Clockwise" Method (Ascending Intervals)
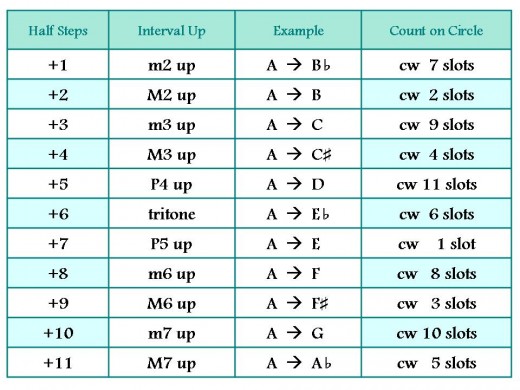
If you already know the name of the interval you wish to transpose, but need to remember how many half-steps are in it, check the information on the tables below.
Look at Table 1 and find the number of ascending half-steps you wish to transpose. Compare this number with the number of spaces on the Circle of Fifths that you will need to move clockwise (fourth column on the table). If the number of half-steps UP that you wish to transpose is an even number, then you will move that exact number of spaces (or "slots") around the Circle of Fifths, moving clockwise from the original key, to find the target key for transposition. In using this tool, you do not count the space where you start.
If the number of half-steps UP that you wish to transpose is an odd number, then you will add or subtract 6 from that number of half-steps and then move that number of spaces (the difference) clockwise around the Circle of Fifths away from the original key, to find the target key for transposition.
Comparison of Half-Steps with Movement on the Circle of Fifths
Some Examples
For example, start at D major; if you wish to transpose up a m3, first convert the m3 to half-steps = three half-steps (an odd number). That is smaller than 6; so add six, with 9 as the sum. Move that number of spaces (9) from D in a clockwise direction and that gives you F. D up to F is a minor third.
If you wish to transpose from F UP a M6, you are moving 9 half-steps (also an odd number). Since nine is larger than six, subtract 9 - 6, for a difference of three; then move three spaces clockwise around the Circle of Fifths, and that brings you to D. If you transpose F up a major sixth, you will transpose to the key of D. (Notice that D --> F ascending = m3; F --> D ascending = M6. The m3 and M6 intervals are inversions of one another. More on that below.)
If you wish to transpose from D UP a m7, that will be ten half-steps. Since ten is an even number, count ten clockwise from D and you reach C. If you transpose from C UP a M2, you will move two slots or spaces from C, since the M2 is two half-steps, and you will reach D. (The M2 is the inversion of the m7.)
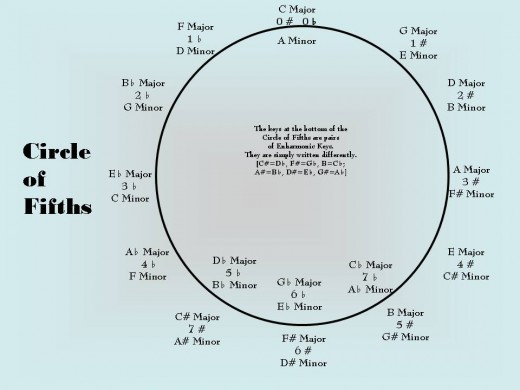
The Circle of Fifths
WARNING!
WARNING!
Super-Geekiness Ahead!
Read at Your Own Risk!
"Shortest Distance" Method (Including Interval Inversions)
You probably noticed that if you always move clockwise around the Circle of Fifths (when you are transposing up, or in the ascending direction), you may be taking the long way around to get to a space that is fairly close to the original. There is another pattern for moving around the Circle of Fifths, but it is more complicated and not for the faint of heart.
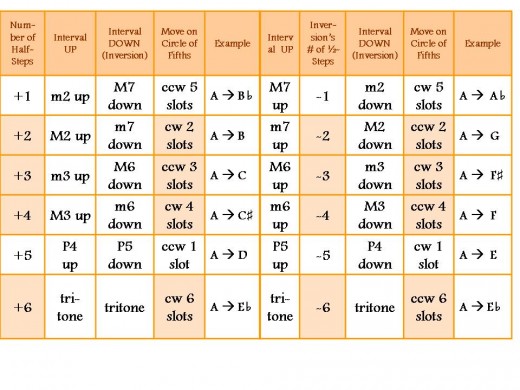
Table 2 lists half-steps only through six, but in either direction: "+" for ascending intervals and "-" for descending intervals. Both the actual interval and its inversion are listed next to the number of half-steps moved. So, for example, one half-step above the original note (or key) is a minor second (m2) higher; that is the inversion of the M7. B up a minor second brings you to C. B down a M7 brings you to C. (Also, C UP a M7 brings you to B; C down a m2 brings you to B. Whew! Are we there yet?....)
Notice that in the "Move on Circle of Fifths" column, both directions around the Circle are given, so that we can find the shortest distance. As with the previously described method, there are some curious correlations between the number of half-steps moved and the number of spaces around the Circle. Again in this case, even numbers of half-steps move clockwise the same number of slots to find the new key; odd numbers move counterclockwise a small odd number of spaces, but the numbers reverse the counting sequence. (Up one half-step, count ccw 5; up three half-steps, count ccw 3; up five half-steps, count ccw 1.)
With larger intervals, the correlation between half-steps and number of slots moved relies on the number of half-steps in the inversion of the interval; and the directions on the Circle are reversed. Even numbers of half-steps still move the exact same number of spaces, but in the counterclockwise direction. Odd numbers of half-steps now move clockwise, but again reversing the counting sequence (1 half-step counts 5; 3 counts 3; 5 half-steps counts 1).
For example, if you wish to move from C up M3, you will move +4 half-steps; since this is the "+" direction, you will move clockwise, and since 4 is even, you will move 4 spaces. [C] - G - D - A - E. C up M3 = E. If you want to move from E up a m6, look at the inversion of the m6; that is the M3 down, or -4 half-steps. Since it is a "-" direction and even, you will move counterclockwise 4 spaces (back to C). Remember that the pitches must be a m6 above the original note, so you want the C that is above the starting E, not the one below.
If you wish to move from E up m2, you will be moving +1 half-step; since it is "+" and an odd number, you will move counterclockwise five spaces. [E] - A - D - G - C - F. If you wish to move from F up M7, look at the inversion of the M7; that is the m2 down, or -1 half-step. Since it is in the "-" direction and an odd number, this time you will move clockwise five spaces (back to E).
Moving the Shortest Distance in Either Direction
In the final analysis, is there really any advantage to taking the time or mental energy to learn these patterns? Maybe so, maybe not. On the Circle of Fifths, we already know that the interval of a P5 ascending is found as the next key clockwise on the Circle; and the interval of a P4 ascending is found as the next key on the Circle in the counterclockwise direction.
The patterns described above in this article are very interesting, and for students and musicians who enjoy that sort of thing, it may be a fun exercise to see these relationships between notes and keys in a new light. Like any tool in any other field of endeavor, the more often it is used, the better one can judge how useful it actually is. The biggest use that I predict for this would be for those musicians who don't have a strong background with a keyboard instrument and who need an additional source of checking to be certain about the precise interval between two notes or keys.
I welcome all feedback. Thanks for reading!
More about the Circle of Fifths and Intervals
- New Uses for the Circle of Fifths
The Circle (Cycle) of Fifths (Fourths) is a delightful and elegant visual representation of relations between musical keys. The exact name for it depends partly on the area of the English-speaking world where you live. - The Cycle of Fifths
The Cycle of Fifths is the key to understanding Western music. It is truly a thing of beauty in its symmetry, simplicity and fruitfulness. As a Classic Guitarist, the cycle of fifths has taught me a great deal. by Paraglider - Music theory cycle of fifths
Knowing the intense hatred most people have for music theory, I'm going to keep this very simple. Starting with the key of C at the top of the circle - C has no flats or sharps. by Jon Green





