Understand Chords: Beyond Seventh Chords To Chord Extensions--Ninths, Elevenths And Thirteenths (Part Four of a Series)
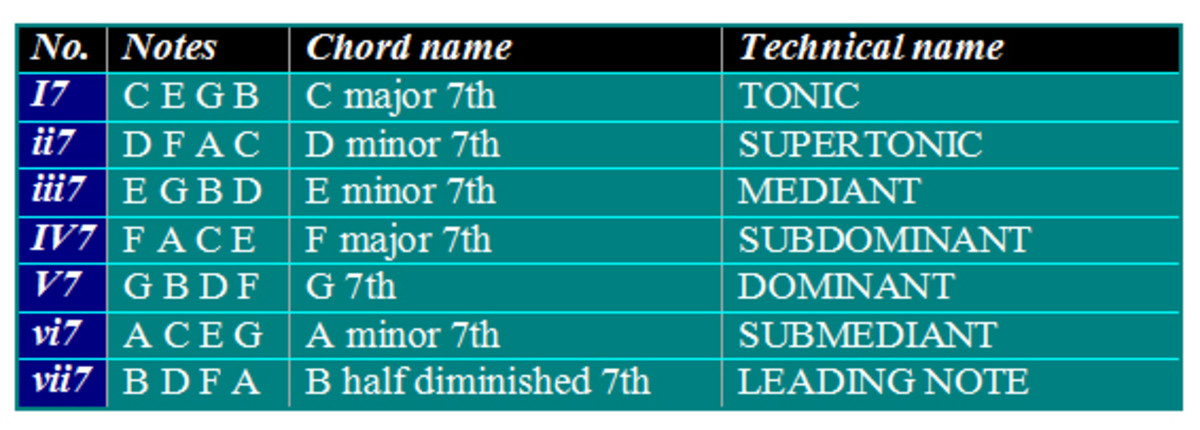
In previous “Understanding Chords” articles we’ve considered what are called “tertian chords”—chords formed by stacking notes that are separated by the interval of a third. By stacking thirds we first formed three-note “triads” and then four-note “seventh chords.”
For example--and to continue our quick review--suppose we begin with the A natural minor scale, consisting of the tones A-B-C-D-E-F-G-(A). We start with the third A-C, comprising tones 1 and 3 of the scale. (Technically, these are referred to as “scale degrees.”) On top of this third, we then stack the third C-E—scale degrees 3 and 5. This three note chord, or triad, A-C-E, is called the “A minor” triad (or chord.)
Notice how it is named according to the lowest of its three tones, the “A.” This tone is referred to as the “root” of the triad; the other tones are named in relation to it as the “third” (C) and “fifth” (E). By convention, this is true even if we reshuffle the triad so that the C or E becomes the lowest actual tone; the root is still the lowest tone in the idealized “stacked third” form of the chord, and the name of the chord does not change.

We can extend this process a step further by adding another third, E-G, to form an A minor seventh chord upon the same root. It sounds a bit more complex and a bit more unstable than the A minor triad. Seventh chords such as this one are particularly favored in jazz harmonies, where they are generally more common than simple triads.
That much is review. But the 'stacking' process can be extended still further. If we do extend it, we'll successively form chords of the 9th, 11th, and 13th. (Hence the term, "extended chords.")
Let’s take our by-now familiar A minor scale as the basis for examples of each of these chords. The 9th chord is formed by adding the third G-B, giving us a five-note chord, A-C-E-G-B; the 11th would be the six-note chord, A-C-E-G-B-D; and the 13th would be a seven-note chord, A-C-E-G-B-D-F.
Here are all three written out. (You can also hear all three by playing the brief video example.)

At this point, we run out of new scale tones to add--the 13th already includes all seven tones of the A natural minor scale! So any new extensions would have to be from outside the scale. But if that were all that there is to say about extended chords, the topic wouldn’t merit an article of its own!
For one thing, we have to consider which scale degrees extended chords may be built upon. As discussed in Part Two of this series (Understanding Chords: Triads In Keys), different chord types characteristically occur upon different scale degrees. Our examples so far have all been built upon the first scale degree, or “tonic”--in this case, that's the note "A."
But historically, extended chords were at first built mostly upon the fifth scale degree, or “dominant.” This degree of the scale is harmonically the strongest, although the tonic is the most stable scale degree. No chord is more characteristic of a particular key than the seventh chord built upon its dominant.
So a more common extended chord in the key of A minor would be E-G#-B-D-F. This is a sound frequently encountered in jazz, where it is usually labeled “E7b9.” (That would be pronounced “E seven flat nine.” And in case you are wondering why the third of the chord is G# and not plain old G, it is because minor key chords usually don’t follow the “natural” form of the minor scale—with which we began, for simplicity’s sake—but rather the “harmonic” form. In the harmonic minor scale, the seventh scale degree (G) is raised a half-step (G#).)
The usual form of the dominant ninth chord in minor keys is this "seven-flat-nine" chord.
We’ll look to chords built upon the dominant for our next few examples, and then consider a few non-dominant extended chords.
But before moving on, the example of the ninth chord raises another issue: The ninth chord above has five tones: root, third, fifth, seventh, and ninth. But what happens when a musician wants to use the sound of a ninth chord, but doesn’t have five ‘voices’ available to sound it?
This could happen more frequently than you might think. The obvious situation would be when there are only four voices or instruments—say, when writing for a vocal quartet, or of saxophones or brass or strings. Could you still write a ninth chord somehow?

Before answering that question, let me add that there are more subtle factors that can limit possible chord voicings, too. For example, the musical logic of the melody and bass line might dictate that they both need to sound the root of the chord—or some other chord ‘member,’ as the different chord tones are called.
But what is the answer to our question, you ask?
Yes, even if you don't have five voices free, it may still be possible to get the ‘ninth chord sound.’ In this case you must write an incomplete ninth chord.
How does that work? Well, not all chord tones contribute equally to the sound of a particular chord. In particular, the fifth of most chords is fairly colorless. Simply leaving it out of the chord will affect the sound only a little. The chord will be a little less full-sounding, but will retain the same essential color and harmonic meaning.
So it is quite reasonable to write a ninth chord without including a fifth, as in these examples:

Let's focus on the second chord for a moment. You can see that it has two root tones in it. We say of chords like this one that the root is “doubled.” The term is also used more generally; “doubling” can be considered a sub-discipline of arranging. The term “voicing” includes doubling, but extends past it to include all aspects of a chord's presentation in a musical piece.
To name some of the aspects, chord tones may be right next to each other, in which case we might speak of “close harmony” or “close spacing,” or they might be widely spread out in “open spacing.” Chords can be massive and thick, with many doublings, or incomplete and airy-sounding. It all depends upon the expressive quality wanted. In fact, the exact ways in which chords are realized can be quite a large part of a composer’s or arranger’s “sound,” and involve creativity and imagination as well as technical skill.
Moving on to the eleventh chord, we find the issues of voicing more critical yet. We have six tones, E-G#-B-D-F-A. The chord itself sounds harsh, or overly dense. We can leave out the fifth, as we did in the ninth chord, but the result is only a bit better.

The biggest part of the problem is the clash between the G# (the third of the chord) and the A (the 11th.) Since we can’t have an eleventh chord without an eleventh, the third is often omitted in order to avoid this clash. (By the way, this is unusual; the third is very important for the 'color' of a chord, and is not usually omitted for this reason.)
Omitting the third gives us a curious chord which looks like a D minor triad with an E bass tone. In fact, popular music often symolizes this chord in just that way, labeling it "Dminor/E." (The triad name comes first, and following the “slash” comes the name of the bass note desired.)
But whether it looks curious or not, this chord—E11 or Dm/E—is normally voiced just as shown here, and transpositions of this voicing form the normal dominant elevenths in all major and minor keys.

Still more extreme are the 'voicing needs' of the dominant 13th. Heard in a complete voicing, it sounds overly thick and heavy—even, perhaps, unfocussed. But a judicious revoicing changes it completely.
We need the 13th, of course, and it is nice to have the root of the chord present. The seventh is an important chord tone. And finally--and as we noted above--the third adds a great deal of color to any chord. Accordingly, our example of E13 includes only four those four chord tones: root, third, seventh a 13th. You might call it radically incomplete, since with four chord tones present and three missing, it is only a bit more 'there' than 'not there!'
But radically incomplete or not, the unfocussed, dense quality of the previous chord vanishes when the chord is rewritten to use only these four chord tones, as shown below.

It’s interesting to note that the upper three chord tones are disposed in stacked fourths. This, it turns out, is a useful voicing in jazz, and can be used in other contexts than that of the thirteenth chord.
But that's another topic. First we should take note that all our extended triads so far have been in minor! Minor mode was a convenient starting point, but in reality major is heard more often. Here are standard major-mode voicings for extended dominants. They are given for the key of A major (three sharps.)

The ninth chord is mellower in sound than the minor-key version, and is usually symbolized simply as E9--not E7b9. The eleventh chord is mellower in major, too, and would be symbolized E11. The thirteenth, like the other extended chords, is a little mellower, a little less plangent, than its minor key counterpart. It's less common to specify the difference in sound, though; both are often symbolized simply as E13, with the player being expected to know that in minor the 13th is usually lowered in minor keys.
The major-key voicing of the dominant 13th shown above is classic, and is fairly common in jazz. But it actually goes at least as far back as the music of Franz Schubert (1797-1828.)
It’s also a somewhat paradoxical beast: the upper three voices form a highly dissonant sonority, yet their harmonic meaning is so well-established that the slightest hint of an appropriate tonal context can evoke the harmonic function of a dominant, even if the root is not present!
This idea of chords presented without roots may seem strange to a Classically-trained musician; Classical practice begins with the notes on the page, and if a note is not present, then why would it ever be considered as a possible root? Few if any analysts in this tradition would look at a triad built on the seventh scale degree, and call it an incomplete dominant seventh chord with a missing root! (See a possible example of this below.)


But things are different in jazz. It is an improvisatory tradition with a long history of chord substitution and alteration. Jazz musicians—pianist George Shearing and saxophonist Charlie Parker come to mind--have been celebrated precisely for their ability to change given harmonies in creative ways. So harmonic identity is, in a way, more fluid and more changeable in jazz.
At the same time, much of the core repertoire of traditional jazz—the so-called “standards”—is highly tonal. (“Highly tonal” means that the harmonies strongly reflect or imply key centers, and that the trajectories of the harmonies mostly follow familiar patterns governed by traditional tonal logic. But the details of that logic are a whole other topic.)
This means that both musicians and experienced listeners intuitively know what to expect, harmonically speaking, as they follow the music's unfolding in time. That expectation allows them to infer chord roots even when they may not physically be sounding.
So in traditional jazz it is not strange to speak of chord voicings which do not include the root. In fact, it’s fairly common for jazz musicians to do so. After all, the root is important for a chord’s identity, but not so much for its characteristic color—and it is the color that performers strive to project, or to manipulate for harmonic effect.
(Of course, from a performer’s perspective there’s another issue. If you are a jazz pianist or guitarist, you may choose to leave out the root--but the bass player can still choose to include it--or not! Inclusion of the root can be a shared responsibility.)
The video example below shows this vividly: there are only a few chordal roots heard, always in the bass, and all are circled.
This example takes avoidance of the chord root to an extreme. The only strong roots are at the phrase endings in measures 8 and 16, where root position dominants are heard on the beat, and on the very last tonic chord. The tonal clarity of the root position chords comes as something of a relief, but overall the functions of the chords are not really in doubt; we still know 'where the music is going.'
The chord roots were avoided in part by making free use of chord extensions to achieve a fuller sound; 9ths are particularly common. For example, in neither of the first two measures is there a root stated, but the piano's D in measure 1, and its G in measure 2 are both 9ths. Analyzed thus, these chords are "rootless ninth chords." (A classically-oriented analyst might well consider them to be seventh chords built on roots a third above the 'absent' ones.)
The last chord, by contrast, is a complete dominant 9th; though the piano does not play the root, the bass does.
This emphasis on 9ths and other extensions, combined with the lack of chordal roots and a prevalence of dissonant ('clashing') harmonies, gives this short tune a rather creepy vibe--despite the 'cheesiness' of the computer-generated tones.
Let’s conclude with a quick look at extended chords not built on the dominant.
Possible 'non-dominant' extended chords aren’t literally endless, but there are enough of them to make a comprehensive catalog dauntingly large. We'll keep the discussion manageable by looking at major keys only—for minor, there are more than twice as many possibilities, and most would be quite rare in actual usage.
We’ll start with ninths. It’s easy enough to take the standard voicing and transpose it to each scale degree successively. The example below shows this written out for the key of C major.

In addition to the dominant ninth, discussed above, we find three types of ninth chords.
Type One, which has a major seventh above the root, is found on scale degrees 1 (C) and 4 (F.) It might be called 'pleasantly tense.'
Type Two is also found upon two different scale degrees, 2 (D) and 6 (A.) It’s characterized by the minor third above the root—that’s the ‘color’ tone of its basic triad. Because chords built upon these two scale degrees are common in jazz, this type of ninth chord is heard fairly frequently as well.
Type Three, like the other two types, has two exemplars: it exists above scale degrees 3 (E) and 7 (B.) But the minor ninth above the root gives it a harsher sound, and it is probably heard less often than Type Two, or even Type One.
Let’s look at the elevenths next.

The elevenths are different from the ninths. As before, we can find similar sonorities built upon 2 and 6 (Type #2 elevenths) and upon 3 and 7 (Type #3 elevenths.)
However, unlike most forms of the dominant, the dominant eleventh is not unique, and instead belongs with Type #2. Type #1, built upon the tonic (C), turns out to be unique, as does Type #4, found upon scale degree 4 (F.) Types #1 and #4 are both fairly harsh-sounding, and probably see less use than other elevenths.
Types 1 and 4 may be tonally ambiguous as well. Most dominant harmonies include scale degrees 4 and 7—the “tritone,” once referred to as “the devil in music.” But though the elevenths upon scale degree 1 and scale degree 4 include that “devilish” interval, neither is supposed to act as a dominant. Thus, these elevenths could send a mixed harmonic message.
The most common elevenths are undoubtedly those of “Type #2,” which, as mentioned above, includes the dominant eleventh.
Turning to the thirteenths, we can observe a pattern generally similar to that of the ninths.

Like the ninths, there is a unique dominant form, and a Type #1 featuring a major seventh found on scale degrees 1 (C) and 4 (F.)
However, Type #2 is represented by a single member, built upon scale degree 2 (D.) The form built upon scale degree 6—in previous cases the same as the chord built upon scale degree 2—turns out to be a member of Type #3 instead. (Type #3 thirteenths are found upon scale degrees 3, 6 and 7.)
At this point, a curious fact begins to be noticeable, though: these standard voicings of elevenths and the thirteenths actually work out to have identical pitch content! Let’s take the chords in turn to show how this works.
The first thirteenth chord consists of the tones A, B, C, and E. Precisely the same tones form the last of the eleventh chords. This is illustrated below.

Similarly, the second of the thirteenths consists of the same tones as the third of the elevenths, and so on throughout the examples. Perhaps it’s easiest to understand if put into tabular form:
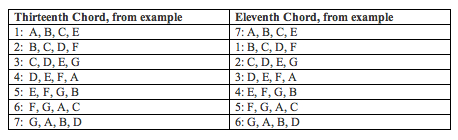
What this means is that in practice there can be considerable ambiguity about whether a particular voicing represents an eleventh or a thirteenth. If the voicing of a chord perfectly follows the standard models shown, we will be able to assign that chord the label 'eleventh' or 'thirteenth,' but many voicings may not conform perfectly. How then will we know which category to apply?
There can even be ambiguity about just what the root is! For example, suppose you find the chord shown in the following example in a jazz chart. It has the same pitch content as the previous example, but is voiced like neither. Which category fits better?

From the improviser’s point of view, this can be an advantage: one can use triad groupings (as in the standard voicings of elevenths) or stacked fourths (as in the standard voicings of thirteenths) quite freely, knowing that they will be interpreted by the ear in the most logical way possible.
Let’s wrap up. We’ve looked at how one constructs extended chords by stacking thirds; we've examined the three possible types of extended chords (ninths, elevenths, and thirteenths); we've compared major and minor key versions of each of these; we've looked at standard voicings for each; and finally, we examined the major key possibilities for each scale step. That’s a lot of material—and as a bonus we uncovered a deep similarity between the elevenths and the thirteenths!
Other Hubs by Doc Snow
- How (Not) To Practice Music Efficiently, Part Two
The nitty-gritty practice secrets and philosophy. Play better, faster! - Inuk Was A-Positive: A Brief Meditation
Sometimes one of those science stories hits you right square in the imagination. - Global Warming Science, Press, And Storms: Nils Ekholm
The fascinating story of a self-made scientist who trusted the data--and saved his own life! - Lavender: The Best Little Asian Bistro In Gwinnett County, GA
The title says it all--but the Hub says it at a bit more length. The best Thai food in these parts! - Sudoku Sherlock-Style: Getting To N-1
Increase your Sudoku-solving skills--and fun! - Pet Doors For Dogs Or Cats: How (Not) To Install Them
Tired of letting the cat out? This Hub shows you how to give your kitty a private entrance.