58
58- 0
Mental Math in Mathematics
- 0
Developing the Quantitative Ability through Mental Activity.
- 0
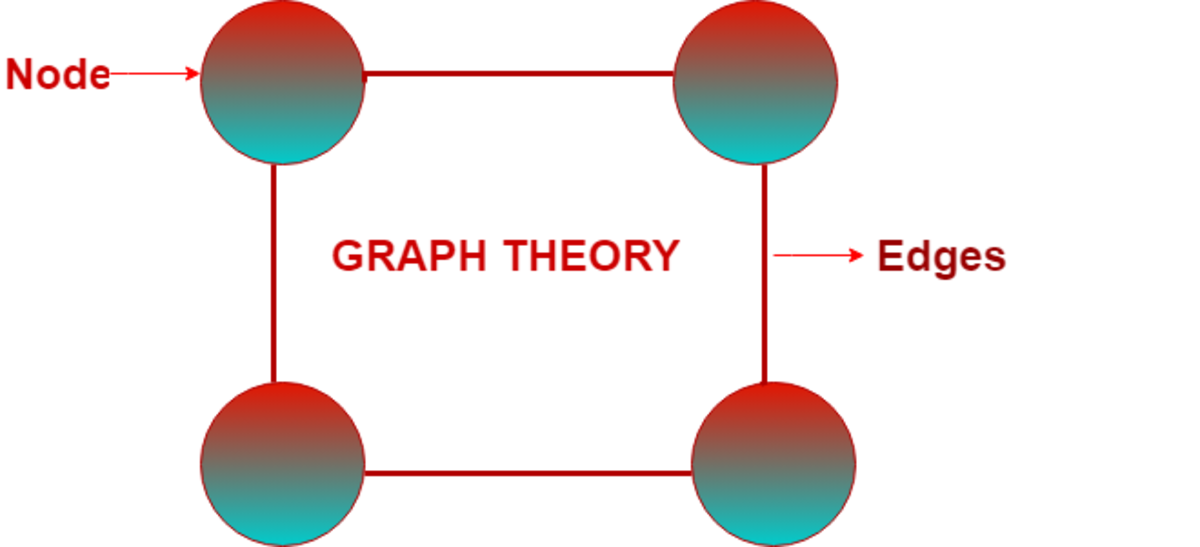
Random Graphs utilizing Hamilton Cycles
- 0
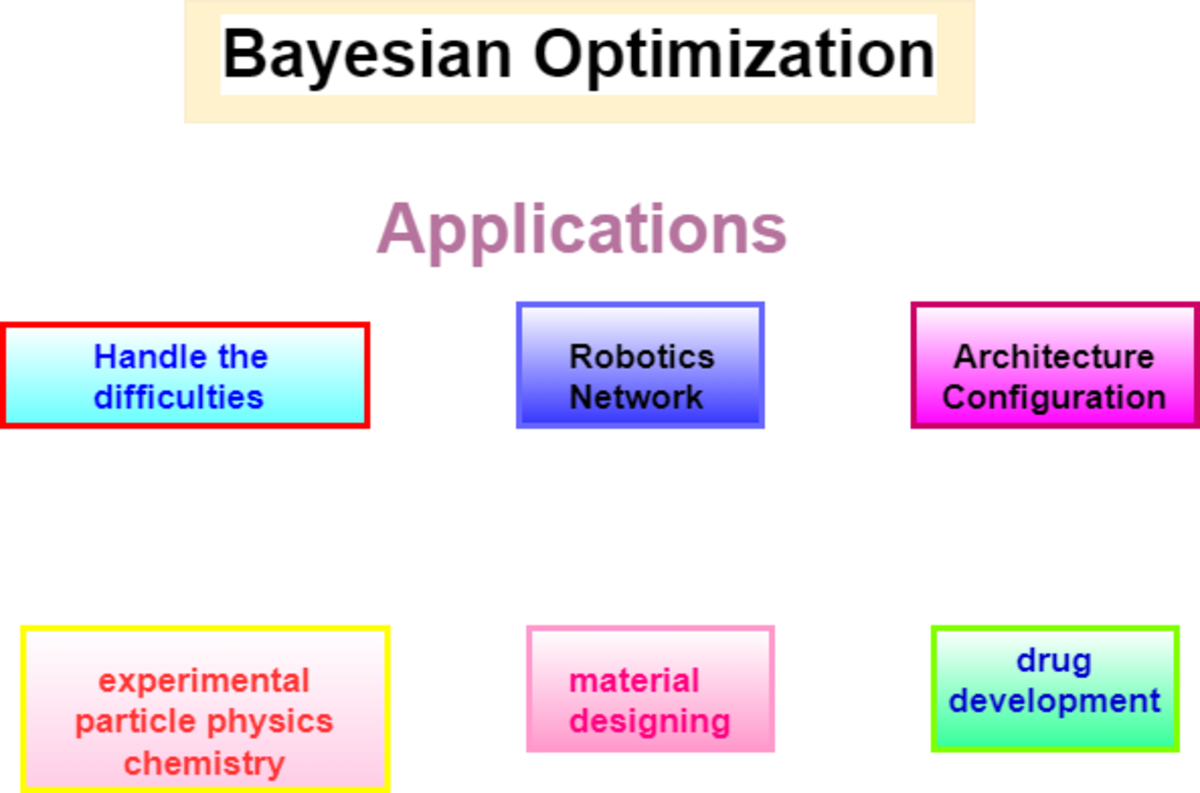
Optimization Bayesian Inversion Using Markov Chain Quasi-Monte Carlo Sampling on Amplitude.
Bayesian optimization is minimizing the number of performed evolutions as well as to optimize complicated and expensive functions. In this article we will learn the definition and applications of Bayesian optimization.
- 0
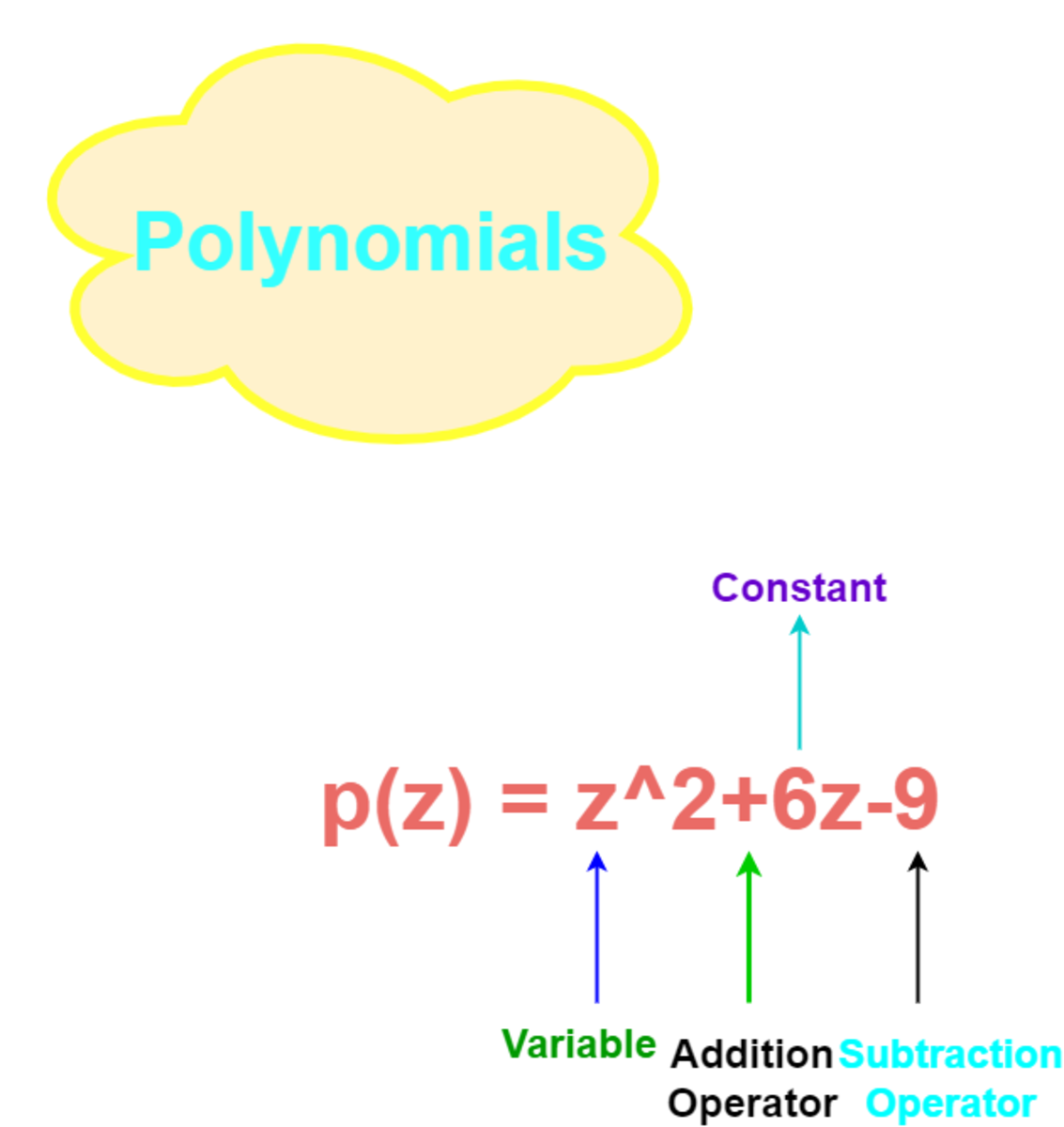
Polynomials (Definition, Types and Examples)
The crucial area of algebra is polynomials. The definition, standard form, degree, and types of polynomials are all covered in this article.
- 0
What are Transcendental Functions?
Transcendental functions are the most important topic of calculus. Here we will learn definition, examples and graphical behavior of some transcendental functions.
- 0
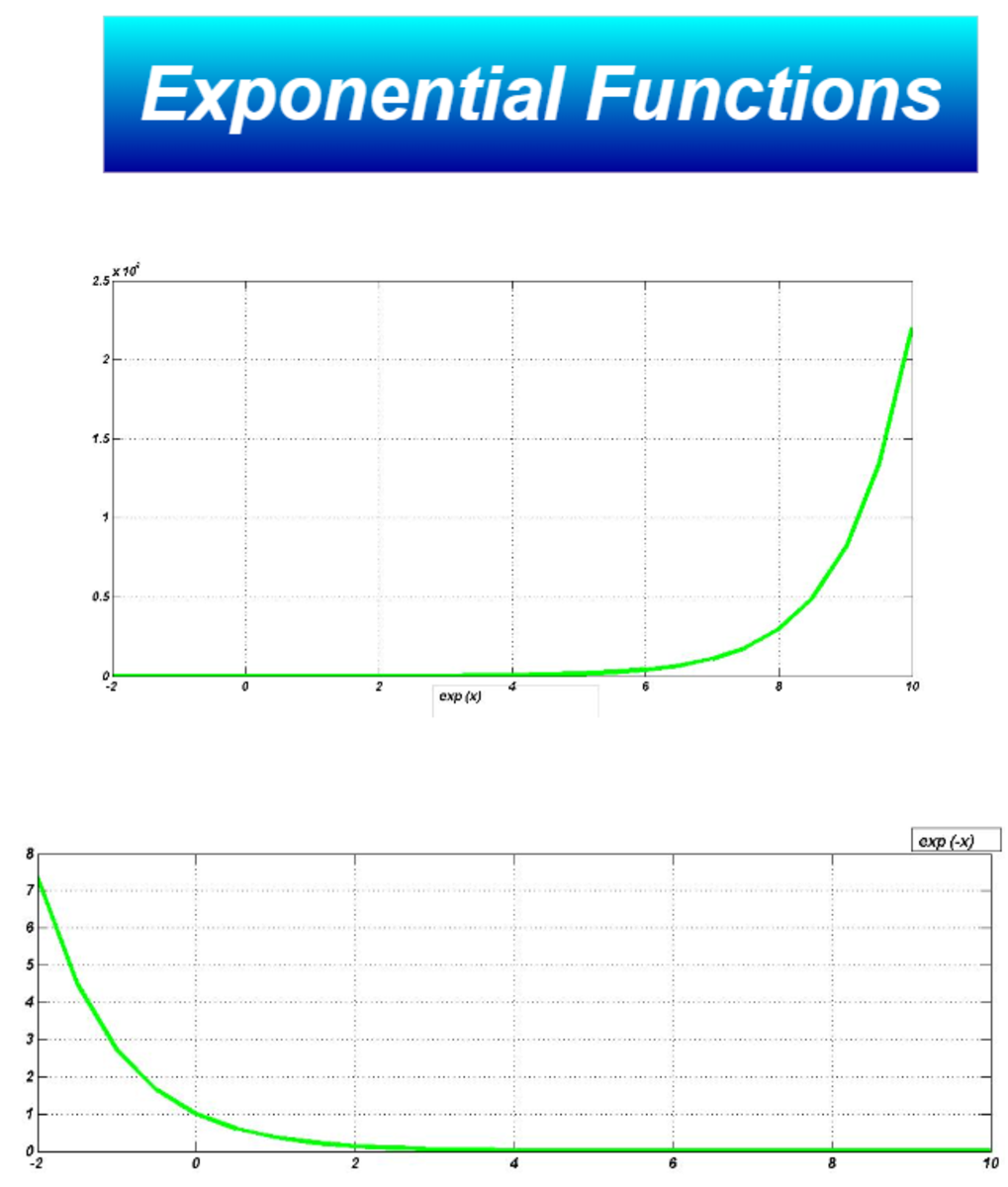
Exponential Functions
Exponential functions are used in our daily life. it is an important topic of mathematics. Here we will learn the definition, basic properties, examples and solved problems of exponential functions.
- 0
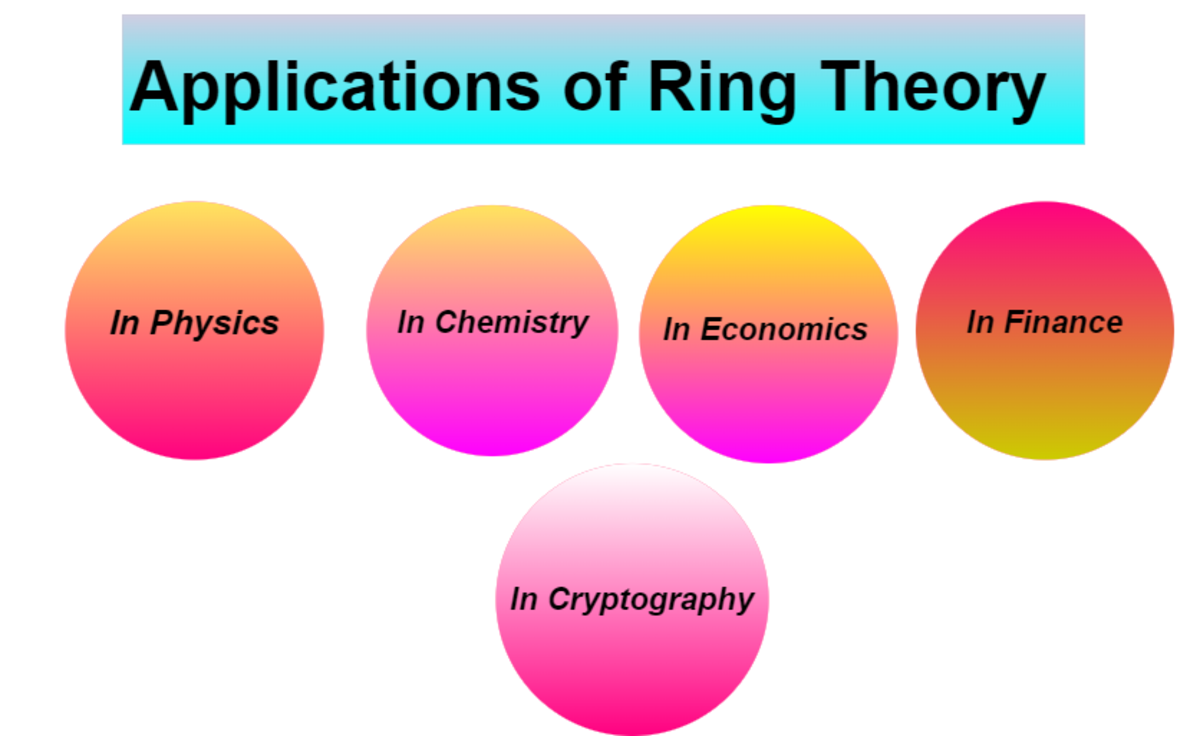
Applications of Ring Theory
Ring theory is important sufficiently that it is also essential in many applications of mathematics. Here we will learn the apploications of ring theory.
- 0
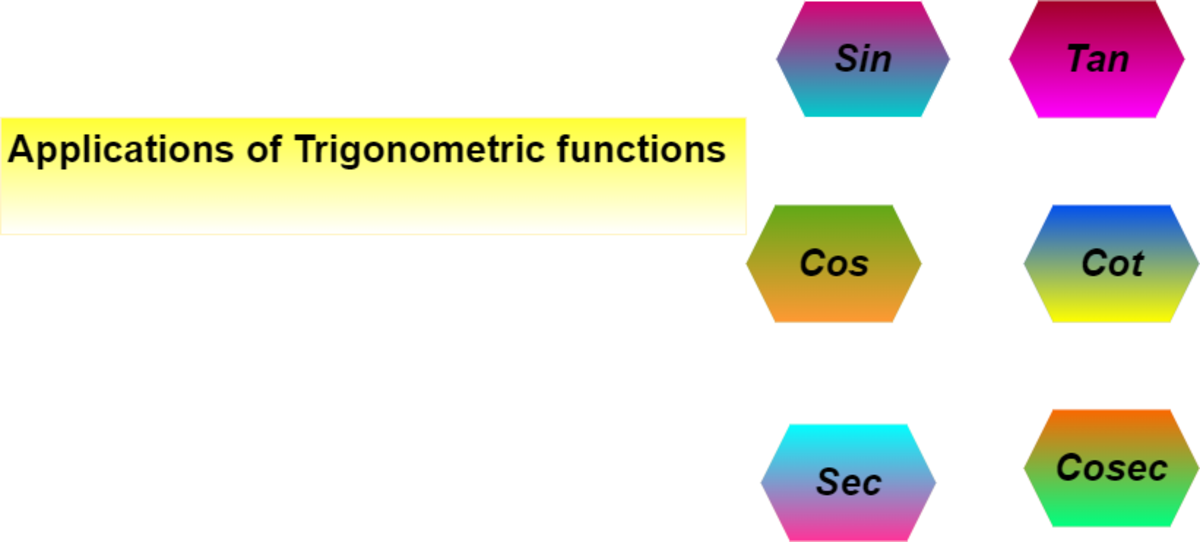
Applications of Trigonometric Functions
Trigonometry is used in every field of life. Here we will discuss the applications of trigonometry in the field of medicine, engineering, chemistry, broadcasting, development of gaming as well as in seismology.
- 0
Applications of Hyperbolic Functions.
All around us, hyperbolic functions play a part in daily life; in this section, we'll discover some of their applications.
- 0
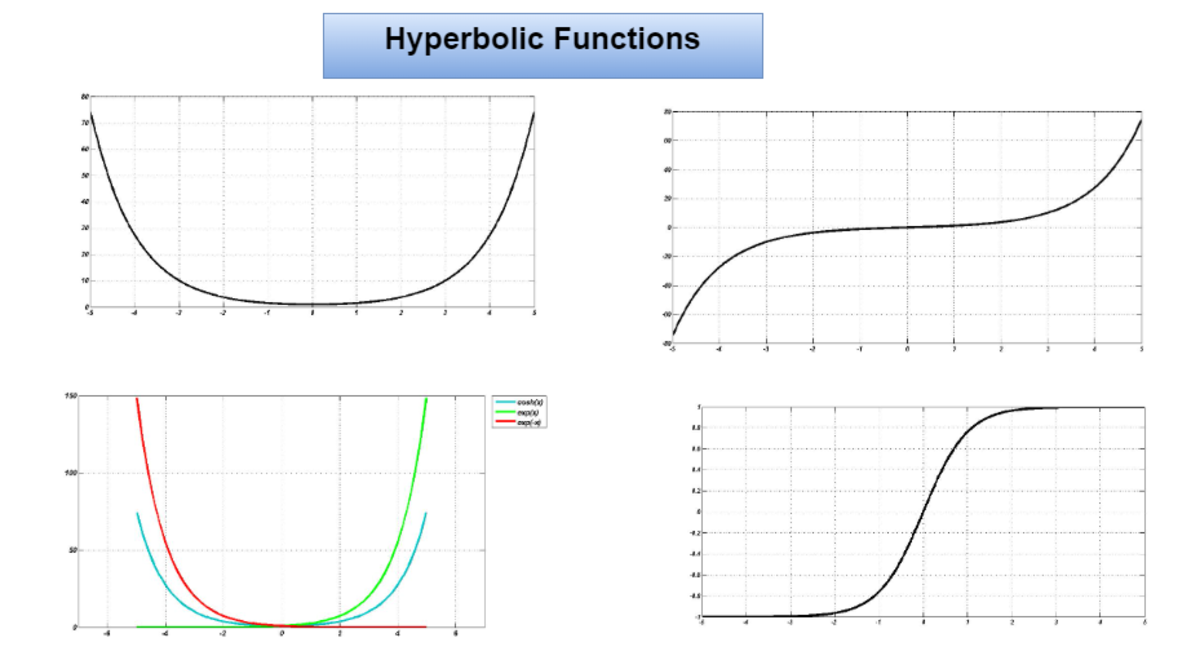
What are Hyperbolic Functions?
Hyperbolic functions are play an important part in mathematics. Here we will learn the definition, basic hyperbolic functions with their graph, identities and examples of hyperbolic functions.
- 0
Trigonometric Functions
The most significant mathematical functions are trigonometric functions. We will learn about its definition, key formulas, and relevant formulas and examples for trigonometric functions and their graphs.
- 0
Techniques Are Used to Find the Indeterminate Form.
Methods for Find the problems of Indeterminate form are used in mathematics to vanish the 7 indeterminate form.
- 0
Method of Rationalization
Method of rationalization is used to solve the difficult questions. This method is used to solve the indeterminate form.
- 0
Method of Factorization to Solve the Equations.
Factorization method for solve the equations is an important method used in every field.
- 0
Indertiminate Forms
Indeterminate forms of limit are most important topic of calculus. There are seven indeterminate forms.
- 0
L’Hospital’s Rule in Calculus
The L'Hospital's rule is the most famous mathematical tool among students because of its effectiveness and simplicity. By L'Hospital's rule we can solve the intermediate forms like 0/0 or ∞/∞ etc.
- 0
Infinite Limits in Calculus
Infinite limits are advanced topic of calculus. It has much importance in every branch of mathematics.
- 0
Concept of Infinity in Mathematics
Infinity is most important term which is used in every field of life as well as every field of science and arts. Everything which is unbounded refer to infinity.
- 0
Continuity and Continuous of a Function in Mathematics.
Continuous of a function is an important topic of calculus. By continuity we can determine the continuity and discontinuity of any function.
- 0
Sandwich Theorem in Mathematics.
Sandwich theorem is a most important theorem of limit. By Sandwich theorem we can comparison of limit of one function to the other function. By sandwich theorem we can find the limit of trigonometric function. Iff three functions are given then find out its limit by sandwich theorem.
- 0
Limit of a Function in Mathematics.
Limits plays an important part in calculus as well as in our daily life. The concept of continuity, derivative and integral is based on limits. It is a most basic concept of calculus.
- 0
Relation between Coefficients and Roots of Quadratic Equations.
Quadratic equations play an important part in every field of life. By Quadratic formula we can satisfy the equation and it tells us weather our solution is wrong or correct. There is basic three methods of solve the roots of quadratic equations by which we can easily solve any quadratic equation.
- 0
The Concept of Quadratic Equations
- 0
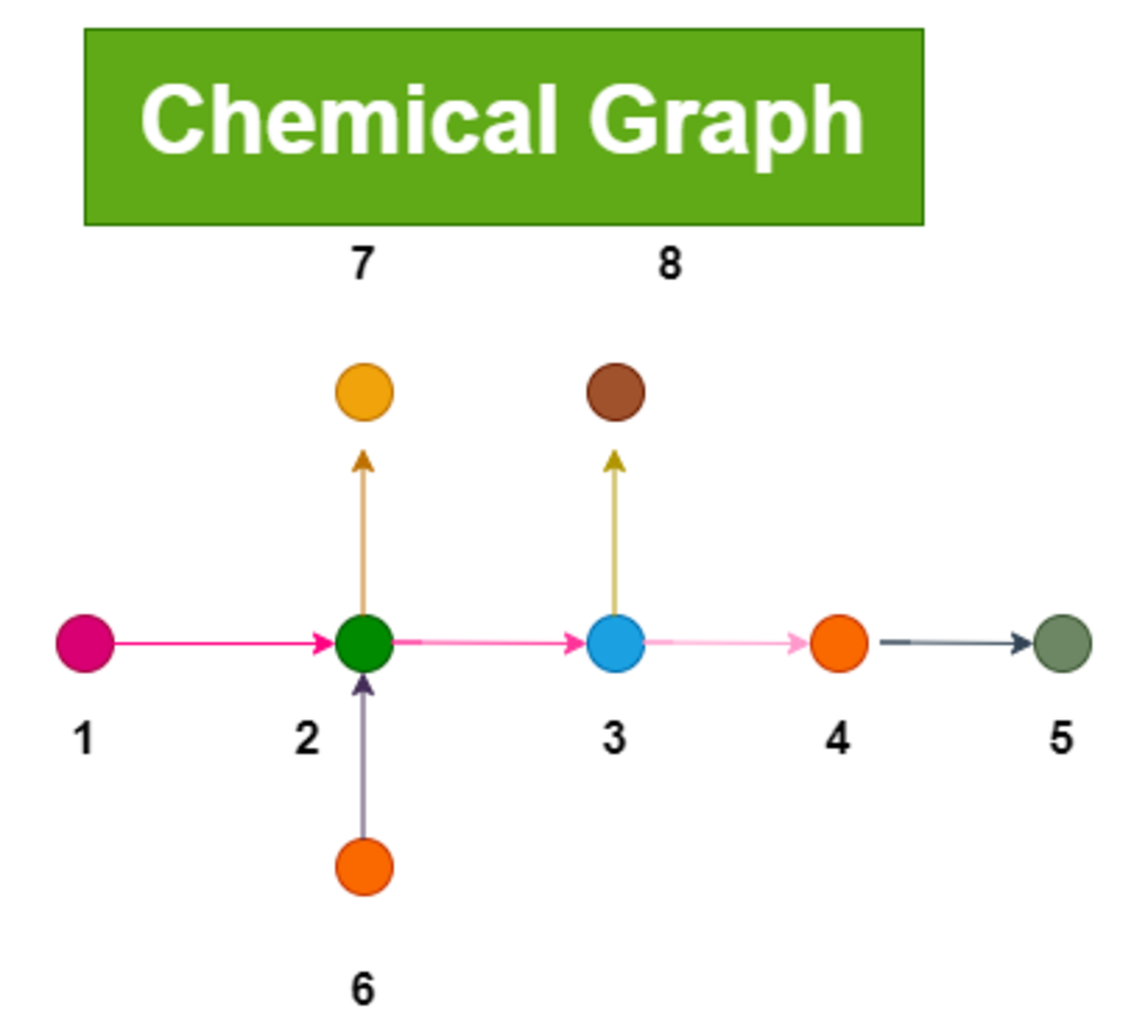
Chemical Graph Theory in Mathematics
- 0
What Is the Concept of Congruences in Number Theory?
Learn all about congruences in Number Theory, as well as the related theorems of Fermat and Euler.
- 0
Euclid's Theorem of divisibility in Number Theory.
- 0
Introduction of Number Theory in Mathematics
- 0
Functions in Set Theory
- 0
What Are Relations in Set Theory?
Learn all about relations in set theory. You'll find helpful definitions and information on four of the most important types of set relations.
- 0
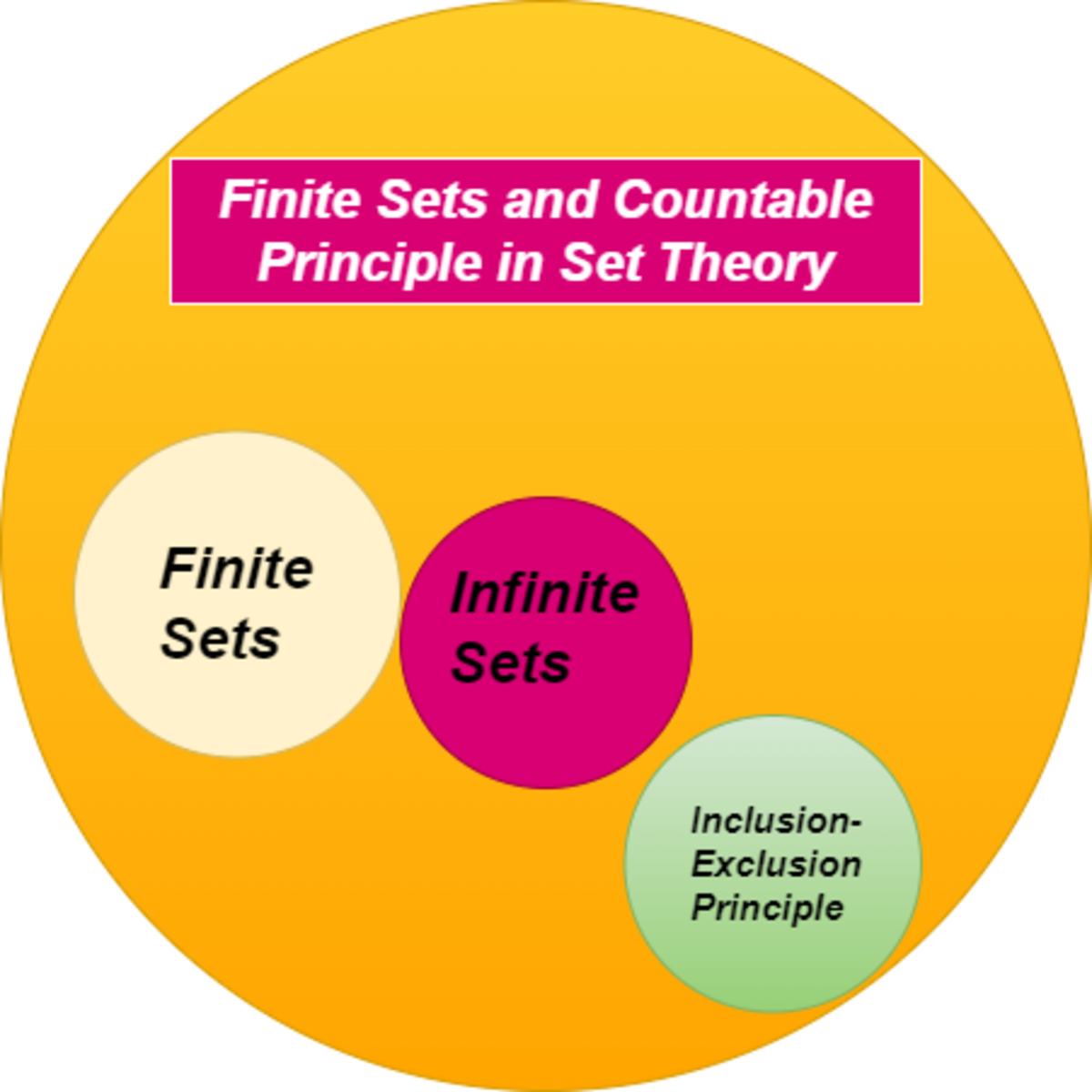
Finite Sets and Inclusion-Exclusion Principle in Set Theory
- 0
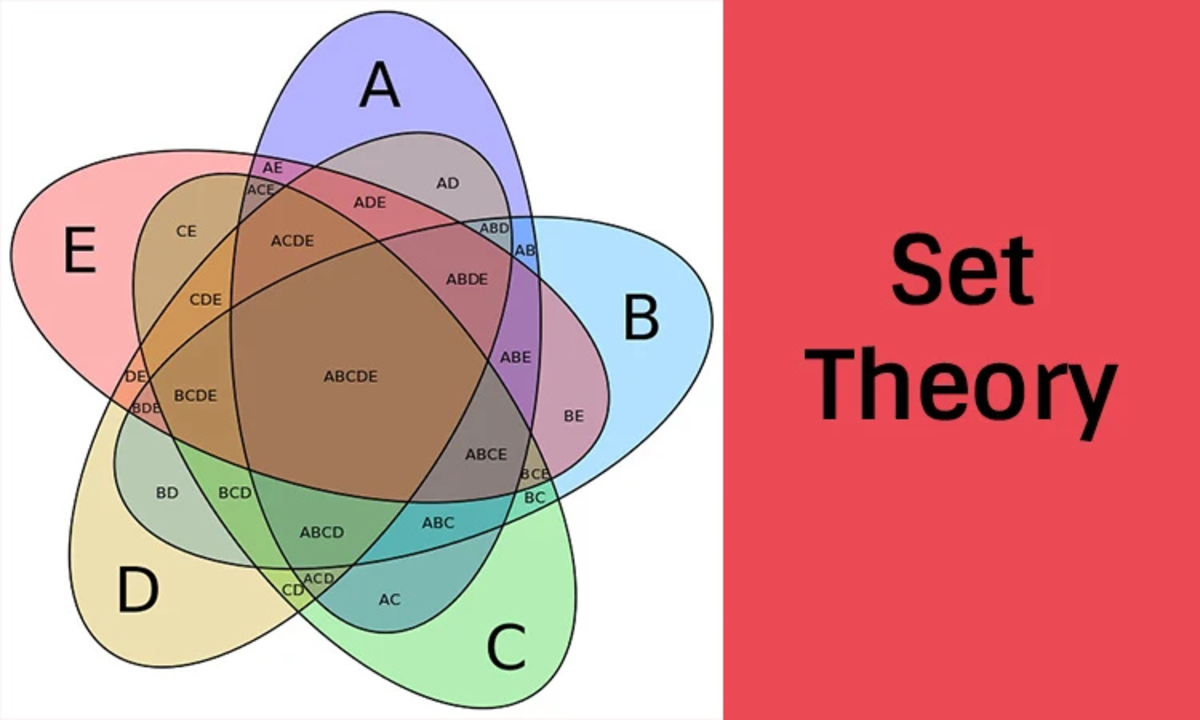
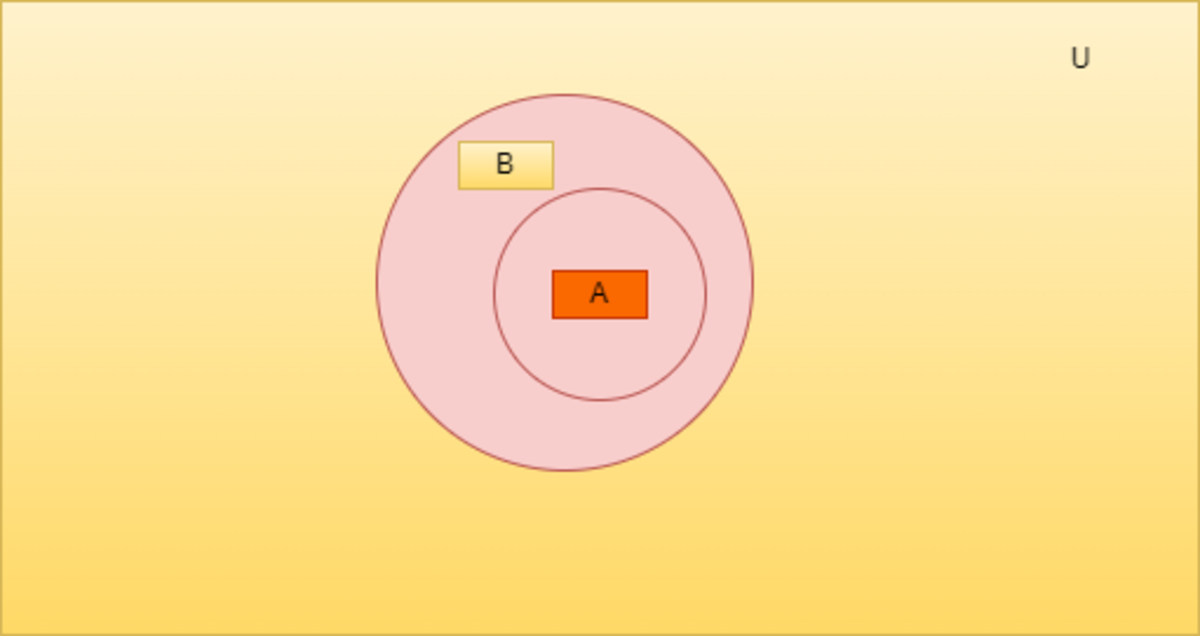
Venn Diagram and Basis Operations in Set Theory
- 0
Set Theory in Discrete Mathematics
Learn about set theory in discrete mathematics, including how to represent sets and subsets. You'll find examples to help you further.
- 0
Applications of Conic Section
- 0
Ring Theory in Algebra
- 0
Importance of Linear Algebra in Computer Science
- 0
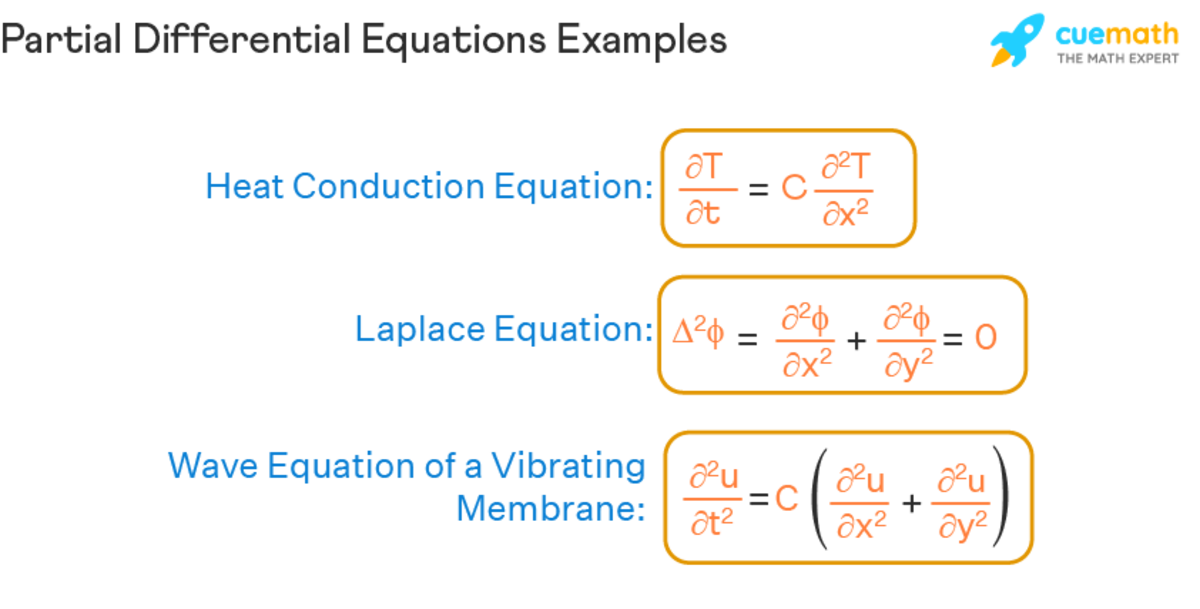
Differential Equations
This article explains differential equations and provides examples.