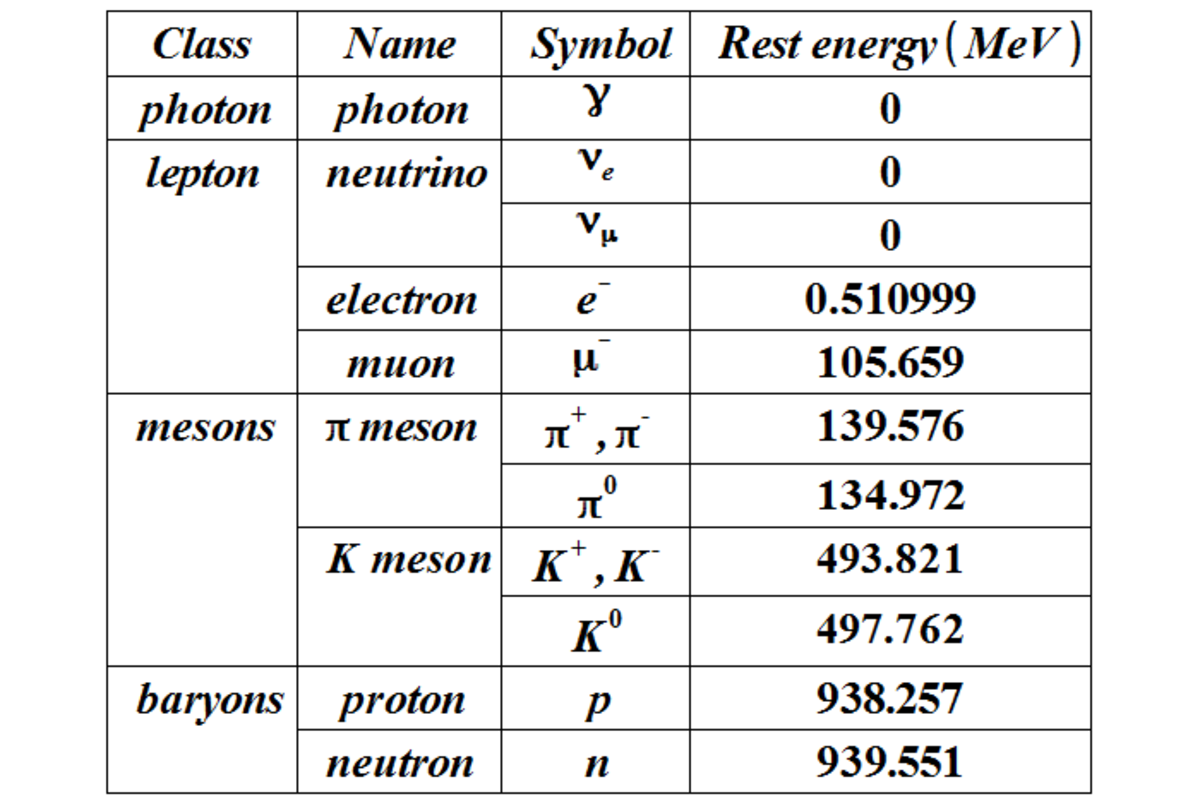
#4evaLIVERPOOL- UNITED
To begin with, this lab report done by LO is aimed at Passive Network 1 and 2. Initially passive networks 2 determining the transient response and frequency response of second LRC networks, in addition to how to interpret data in graphical form and to practice soldering. Thus the lab inclined knowledge of being able to identify a second order system as well as being able to calculate frequency response and time response for RLC circuits in addition to being able to test and record data from a second order system.
Initially, though second order circuits exist in different forms, the behavior of LCR circuits and the examination of the resonant behavior. Thus, the word resonance is defined as the key phenomenon in electronic and electrical engineering because it occurs when a resonant circuit is excited or agitated by a frequency to equal and match to its own natural frequency, which in a layman’s words is a frequency to which makes the circuit respond and react to it in a particular marked way. Thus engineers exploit and manipulate these properties of resonance extensively in many ways; communications, signal processing and power management.
The first experiment done, was a series resonant circuit and being more specific, was to build the RLC series circuit shown in the diagram below.
Once this circuit has been setup, the following procedures were followed and the aim was to test the frequency response LR.
Procedure that was followed;
- Set the signal generator to 1 Vrms and to check with the DMM
- Vary the frequency from 1kHZ to 50kHZ
- Connect the oscilloscope to show Vin and Vr
- Take measurements of Vr increasing the frequency
- At the resonant frequency measure Vr, VL, Vc
- How was the resonance and frequency determined
And to later erpeat all the steps using a resistor with 1.2K ohms
Equipment used;
- Two resistors, 100 ohms and 1.2 kilo ohms
- Capacitor
- Inductor
- Oscilloscope
The accuracy of the oscilloscope used during my experiments as referenced from the internet is below
Oscilloscope
Bandwidth specification
Other amplitude accuracy specification
Keysight DSO6054A
Bandwidth (-3 dB)
DC-500 MHz
DC vertical gain accuracy
±2.0% of full scale
For 100ohm; table LCR
Frequency/kHZ
Vr/V
Vin/V
1
0.250
3.275
2
0.432
3.313
5
1
5.103
10
2.85
4.5625
20
2.45
4.4125
50
1.975
4.5255
Frequency/kHZ
Vr/Vin
1
0.076
2
0.115
5
0.1996
10
0.405
20
0.551
50
0.436
Resonance frequency was determined using the gain (Vr/Vin) vs Frequency . Thus the peak of the graph shows where Vr=Vc shows resonance for at this point Vr = V For 1.2kilo ohms
Frequency/kHZ
Vx/V
Vin/V
1
0.120
3.34
2
0.169
3.90
5
0.260
4.54
10
0.320
4.70
20
0.960
4.30
50
0.320
4.70
Frequency/kHZ
Vr/Vin
1
0.0359
2
0.0410
5
0.0441
10
0.068
20
0.2230
50
0.0680
Resonance frequency was determined using the gain (Vr/Vin) vs Frequency. Thus the peak of the graph shows resonance
Comparisons of plots – Shape and real vs theoretical
= Shape of the graph is in a ‘Bell Shape’ and it was seen that the peak value gives the resonant frequency. Thus the theoretical value of the resonant frequency is more than the real value of resonant frequency.
The Q factor is called the magnification factor or the quality factor. In a layman’s word is the measure of the magnification of the voltage developed across the L and C at resonance compared with the input voltage. The change in frequency of a circuit is defined as the difference between the frequencies at which the power dissipated is half of the power dissipated at resonance.
Estimation of the value of Q value using the formal f/change in f (where F= frequency) and the plot of experimental results
= Q= f/change in f
Q=0.58/(50k-11k)
Q= 1.51*10-1
Comparison of the Q value to the theoretical value
= Q= 1/R (L/C) exp0.5
Q= 1/100(4.7*10-2/0.01*10-6) exp0.5
Q= 0.1874
Thus the theoretical value is a bit higher than the real value of Q. So it is safe to say that the magnification at the voltage developed across the L & C at resonance compared with input voltage.
Another experiment; Parallel LRC
For 100ohms
Frequency/kHZ
Vr/V
1
1.37
2
1.33
5
1.13
10
0.720
20
0.200
50
0.265
100
1.29
200
1.64
500
1.93
Thus the peak of the graph shows resonance
Graph of Vr/V vs Frequency
For 1.2kilo ohms
Frequency/kHZ
Vr/V
1
2.65
2
2.65
5
2.65
10
2.49
20
1.32
50
2.68
100
2.81
200
2.81
500
2.81
Thus the peak of the graph shows resonance
Graph of Vr/V vs Frequency
Thus my Initial Finding with the Parallel LCR in terms off the comparison of plots and the shape and real vs theoretical.
= The graph was a “U “ shape and the real graph is more steeper than the theoretical graph.
To conclude, referencing an article on google about oscilloscopes and their errors online, an experiment is not 100% accurate due to errors within the instrument and the experimenter thus it was not a 100%.
For, there are many sources of error when operating the oscilloscope such as calibration error and the analysis error. The accuracy of the components used within the oscilloscope and can be assumed to be 5% for both voltages and times.
The final results from the accuracy with which a reading can be made from the screen, and is often related to the line width of the trace. Merging the calibration and analysis errors find the total error of any reading. In most cases the reading error will be considerably smaller than the calibration error.
Comparably the error when setting up a waveform on a signal generator will be due to the adjustment error which is 5% and a setting error thus, the final is related to the scale and width of the cursor.
As the procedure indicates, compare the parameters of a signal produced by a signal generator and that measured by an oscilloscope. In this case both the voltage and frequency which involve errors as set on the signal generator should be compared with the values determined by the oscilloscope.
However, Passive Networks 1 is determining the transient response and frequency response of first order LR and RC networks, in addition to how to interpret data in graphical form and to practice soldering. Thus the lab inclined knowledge of being able to identify a first order system as well as being able to calculate frequency response and time response for LR and RC circuits in addition to being able to test and record data from a second order system.
Thus, Once this circuit has been setup, the following procedures were followed and the aim was to test the frequency response LR.
Procedure that was followed;
For the Frequency Response LR
- Set the Signal Generator to 1V peak
- Vary the frequency from 1kHZ to 500Khz
- Connect the oscilloscope to show Vin and Vout
- Take measurements of Vout increasing the frequency in multiples of 1,2,5&10
- Calculate the log of the frequency
- Calculate the gain (Vout/Vin)
- Plot a log-lin graph of log (frequency) against gain
- Identify the corner frequency
- Calculate the real value of inductance from the corner frequency and compare to that identified by the coloured bands
Finding the time constant LR
- Set the Signal Generator to 5Vpeak, square wave, 10kHz
- Connect the oscilloscope to show Vin and Vout
- Measure the rise time of Vout (from 10% to 90%)
- Set the trigger level 50%, adjust Horiz and Vert scale to display one cycle
- Measure the rise time
- Measure the fall time
- Calculate the time constant
- Calculate the real value of inductance from the corner frequency and compare to that identified by the coloured bands.
Time constant RC
- Set the Signal Generator to 5V peak, square wave, 10kHz
- Connect the oscilloscope to show Vin and Vout
- Measure the rise time of Vout (from 10% to 90%)
- Set the trigger level 50%, adjust Horiz and Vert scale to display one cycle
- Measure the rise time
- Measure the fall time
- Calculate the time constant
- Calculate the real value of inductance from the corner frequency and compare to that identified by the coloured bands.
Frequency Response RC
- Set the Signal Generator to 1Vpeak
- Vary the frequency from the 1kHZ to 500kHz
- Connect the oscilloscope to show Vin and Vout
- Take measurements of Vout increasing the frequency in multiples of 1,2,5&10
- Calculate the log of the frequency
- Calculate the gain (Vout/Vin)
- Plot a log-lin graph of log (frequency) against gain
- Identify the corner frequency
- Calculate the real value of inductance from the corner frequency and compare to that identified by the coloured bands.
Data Table RL; Freq vs Vout
Frequency/kHz
Vout/V
Log(frequency)/kHz
Vout/Vin
1
2
0.0
2
10
2
1.0
2
50
1.8
1.7
1.8
100
1.7
2.0
1.7
200
1.2
2.3
1.2
300
0.8
2.5
0.8
400
0.6
2.6
0.6
500
0.4
2.7
0.4
Data Table RC; Freq vs Vout
Frequency/kHz
Vout/V
Log(frequency)/kHz
Vout/Vin
1
20
0.0
20
10
20
1.0
20
50
20
1.7
20
100
18
2.0
18
200
13
2.3
13
300
10
2.5
10
400
10
2.6
10
500
3.6
2.7
3.6
Initial findings
LR Corner Frequency; 350 kHZ
LR Measured value of Inductance; 4700 ohms
LR Rise time; 3.0 microseconds
LR Time Constant; 2.4 microseconds
LR Measured Value of Inductance; 4700 ohms
RC Corner Frequency; 96711 Hz
RC Measured value of Capacitance; 2.2nanoFarad
RC Rise; 1.6 microseconds
RC Fall time; 2.8 microseconds
RC Time Constant; 0.79 microseconds
RC Measured Value of Capacitance; 2.2 Nano Farad