A Simple Formula for Finding the Volume of a Sphere
June 25, 2012

Summary
This article discusses an alternative formula for finding the volume of a sphere (shown below).

This article explains how the formula was derived and how it can be extended to be used with circles and multidimensional spheres.
Intro
I was sitting around the other day wondering how it is one could calculate the volume of a sphere if they didn't know the formula for it. Say if it were 400 BC for instance before the genius of Archimedes figured it out.
A simple solution would be to construct a box with edges all equal to the diameter of a sphere, fill the box with water, press the sphere into it and then remove it. The amount of water displaced would be equal to the volume of the sphere, which you could calculate by determining the rectangular volume of the void. If you did this you would find that the volume of the void (and therefore the sphere) was 52.3% of the volume of the total box.

That is a nice simple formula. It is simpler and easier to work with than the formula for the sphere that we use.

I am certain others have come up with this before, but I have never seen it anywhere else.
The formula we use, of course, has a significant advantage. By using the constant Pi, the formula represents the EXACT volume of a sphere, whereas the alternative formula which uses 0.523 is only an approximation. This is especially important when performing algeabraic calculations on volumes of spheres. To illustrate this let's multiply the volumes of three spheres together.
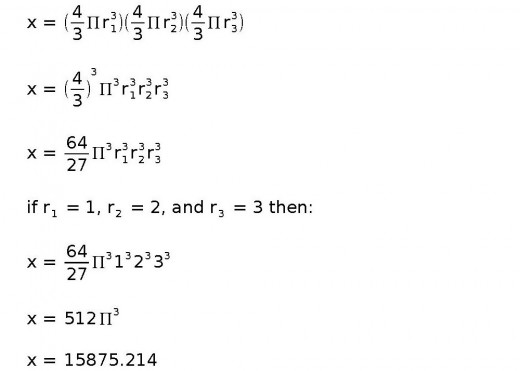
Let's do the same thing with the alternative formula.

You can see that due to rounding errors the alternative formula is off from the more precise volume calculated with the original formula.
But there isn't any reason we can't replace the 0.523 with a constant similar to Pi. We could call this constant the Sphere Constant and represent it with the Greek letter sigma (σ). The alternative formula will then look like this:

Now that's about as simple and as clean a formula as you could ask for, but what is σ equal to. In order to find out we can set the two formulas equal to each other and solve for σ.
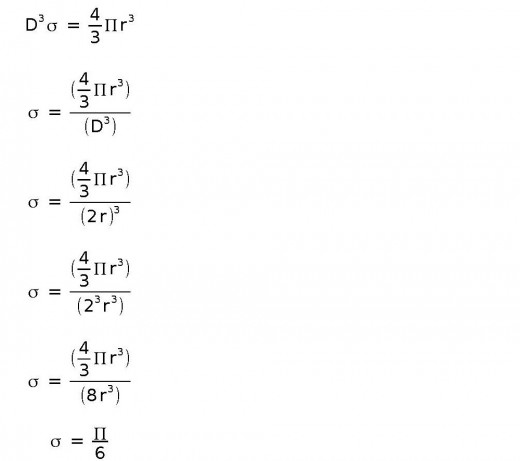
We can use this clean variation of the alternative formula to multiply the volumes of our 3 spheres together.
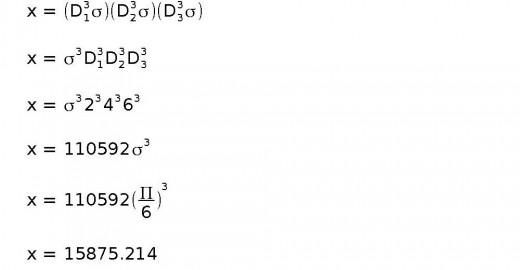
This formula arrives at the exact same answer as the other, but is simpler and cleaner to use.
Additionally, this revised formula can be extended to circles and multidimensional spheres by adding a subscript to the Sphere Constant which represents the dimension of the object.

so that:

I really don't know anything about extra-dimensional spheres, so I can't say for sure that the alternative formula is correct for them, but I really don't see any reason why it wouldn't be.