ANCIENT INDIAN MATHEMATICIANS
Baudhayana
( 800 BC - about 740 BC)
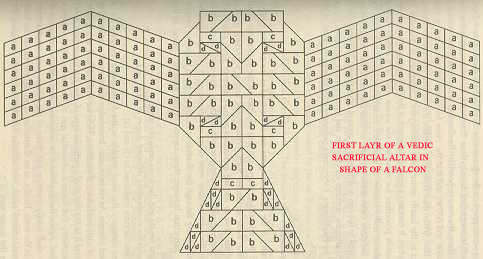
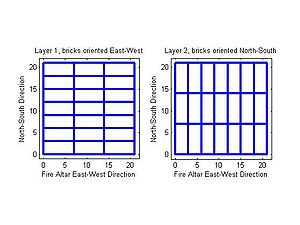
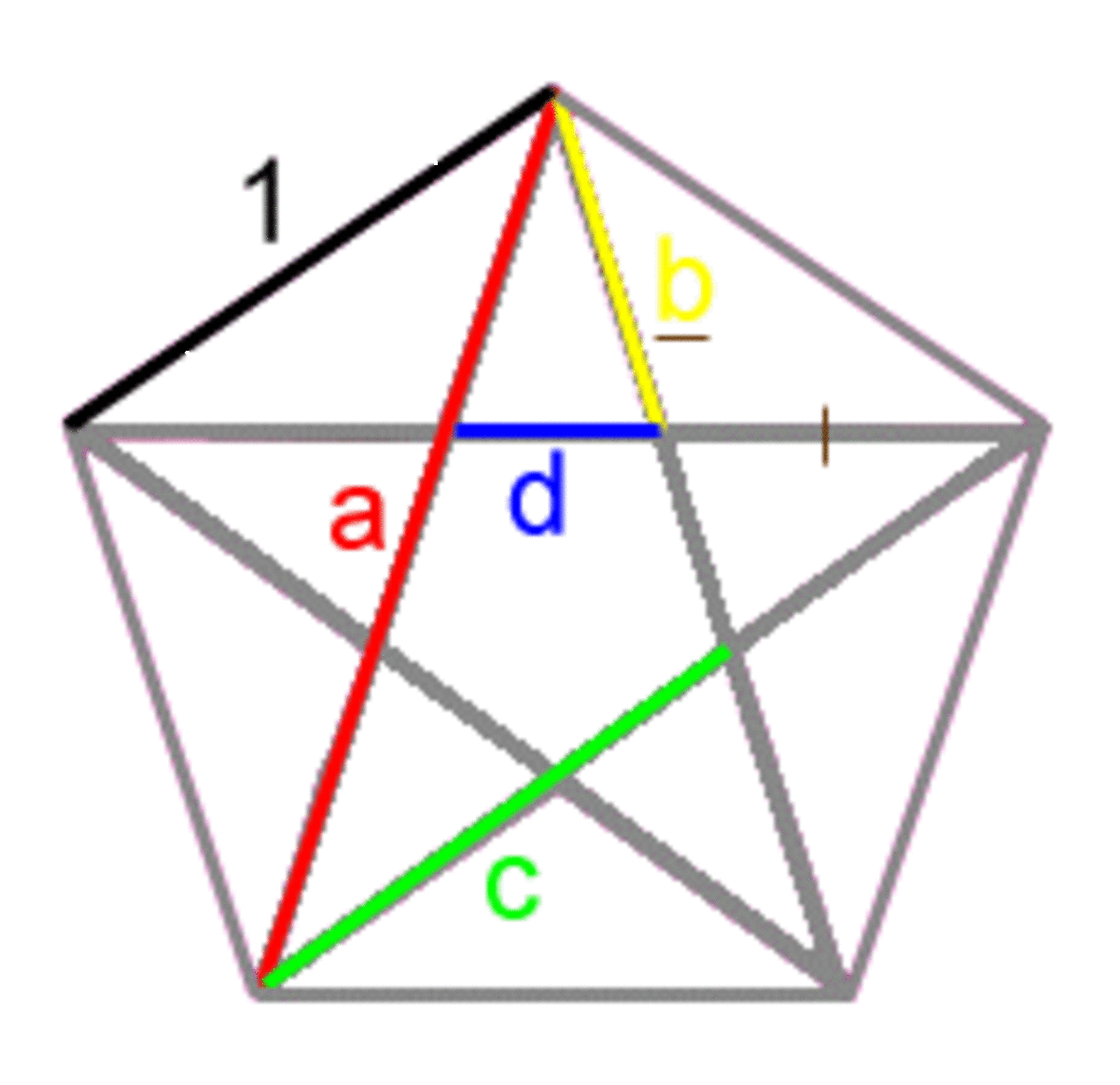
.Nothing much is known about Baudhayana, apart from the fact that he was a priest and a skilled craftsman. His interest in mathematics must have purely for ritualistic practices like construction of altars for sacrifices and mundane needs of a craftsman. In the Sulbasutra of which he was the earliest contributor, we find geometric solutions to linear equations of a single unknowns and approximate values of √2 correct to five decimal places. Though there are several values of π mentioned in Baudhayana's Sulbasutra, the nearest is 900/289 = 3.114
Manava
(750 BC - about 690 BC)
Manava Sulbasutra was not only brought out much later than Baudhayana’s Sulbasutra, but is also a minor one. His work contains approximate constructions of circles from rectangles, and squares from circles. In Manava’s works he was able to calculate the value of π = 25/8 = 3.125.
Apastamba
(600 BC - about 540 BC)
Like Budhayana and Apastamba, is a shadowy figure of antiquity about whose personal life nothing much is known. In his version of Sulvasutra, there are six chapters and he was able to solve the The general linear equation 1 + 1/3 + 1/(34) - 1/(3434). In his work he also tries to dividing a segment into 7 equal parts and attempted the problem of problem of squaring the circle.
Panini
(520 BC - about 460 BC)
Panini was born in Shalatula a town on the banks of the river Indus which is now in modern Pakistan. He was a Sanskrit grammarian whose major contributions were in the field of phonetics, phonology, and morphology. Much of the algebraic nature of Indian mathematics arose as a consequence of the structure of the Sanskrit language. Mathematics in fact was an outcome of linguistic developments in India and Panini laid down the formal rules and definitions of Sanskrit grammar which gave it its linguistic perfection.
Panini's major work is a treatise called Astadhyayi (or Astaka ) . Panini was a forerunner of the modern formal language theory used to specify computer languages. Though The Backus Normal Form was discovered independently by John Backus in 1959, Panini’s notation is equivalent in its power to that of Backus and has many similar properties.