Advanced Proofs of the Dot and Cross Products for Calculus
Vector Bisection
Vectors have so many properties that make their versatility endless and crossover into several disciplines. Sometimes we add them or subtract them, sometimes we take the dot product to find a scalar or a cross product to find a perpendicular vector to two other ones, but other times we may be interested in finding a vector that bisects two vectors. How could we make such a vector? Below we will show how to find that vector which bisects a and b, which happens to be c = ||b||a + ||a||b (Larson 772).
To find such a vector (let’s call it c), I need to remember that it will be the same number of degrees from a as it will be from b. Using one of the definitions for the dot product, I know that
Cos Θ = (c ∙ b)/(||c|| ||b||)
And
Cos Θ = (c ∙ a)/(||c|| ||a||)
But since this is the same number of degrees, both cosine terms will equal each other. Therefore
(c ∙ b)/(||c|| ||b||) = (c ∙ a)/(||c|| ||a||)
Or after eliminating the common term ||c||
(c ∙ b)/(||b||) = (c ∙ a)/(||a||)
Multiplying both sides by ||a|| ||b|| gives us
||a||(c ∙ b) = ||b||(c ∙ a)
And upon expanding the dot product we arrive at
||a||(c1b1 + c2b2 + c3b3) = ||b|| (c1a1 + c2a2 + c3a3)
Distributing the outside term results in
||a||c1b1 + ||a||c2b2 + ||a||c3b3 = ||b||c1a1 + ||b||c2a2 + ||b||c3a3
And after moving all the terms to the left-hand side we have
||a||c1b1 -||b||c1a1 + ||a||c2b2 - ||b||c2a2 + ||a||c3b3 - ||b||c3a3 = 0
Pulling out common c terms will give us
c1(||a||b1 -||b||a1) + c2(||a||b2 - ||b||a2) + c3(||a||b3 - ||b||a3) = 0
Now, some may remember the definition of the conjugate. If I have a (x + y) term, if I multiply it by (x - y), I get x2 + xy – xy – y2 = x2 – y2. Simply put, I multiply by the same term but I change the operation being done to the opposite partner, often in hopes of simplifying further algebra. Therefore, if the components of c are conjugates, then
c1 = ||a||b1 + ||b||a1, c2 = ||a||b2 + ||b||a2, and c3 = ||a||b3 + ||b||a3
Plugging these back in to our equation gives us
(||a||b1 + ||b||a1 )(||a||b1 -||b||a1) + (||a||b2 + ||b||a2)(||a||b2 - ||b||a2) + (||a||b3 + ||b||a3)(||a||b3 - ||b||a3)
= ||a||2b12 -||a||b1||b||a1 + ||a||b1||b||a1 -||b||2a12 + …
= ||a||2b12 - ||b||2a12 + ||a||2b22 - ||b||2a22 + ||a||2b32 - ||b||2a32
And after pulling out some common terms we arrive at
=||a||2 (b12 + b22 + b32) - ||b||2 (a12 + a22 + a32)
But b12 + b22 + b32 is the length squared, or ||b||2, and the same applies for the a terms, so
||a||2 (b12 + b22 + b32) - ||b||2 (a12 + a22 + a32) = ||a||2 ||b||2 - ||b||2 ||a||2 = 0
Yes, c is the conjugate, so
c = <c1, c2, c3> = <||a||b1 + ||b||a1, ||a||b2 + ||b||a2, ||a||b3 + ||b||a3> = ||b||a + ||a||b
Vector Difference and the Dot Product
When I take the difference of two vectors, I will have a net vector as my result. It too will have a magnitude to it, but how is it possible for me to relate this length to the dot product? Below we will show that ||a- b||2 = ||a||2 + ||b||2 – 2(a ∙ b) is true (789).
First, note that by definition of vector magnitude,
||a- b||2 = ([(a1 – b1)2 + (a2 – b2)2 + (a3 – b3)2]0.5)2
=(a1 – b1)2 + (a2 – b2)2 + (a3 – b3)2
Expanding this out gives us
(a1 – b1)(a1 – b1) + (a2 – b2)(a2 – b2) + (a3 – b3)(a3 – b3)
= a12 – a1b1 – a1b1 + b12 + a22 – a2b2 – a2b2 + b22 + a32 – a3b3 – a3b3 + b32
= a12 – 2a1b1 + b12 + a22 – 2a2b2 + b22 + a32 – 2a3b3 + b32
And after a little bit of rearrangement, we will have this equaling
a12 + a22 + a32 + b12 + b22 + b32 – 2a1b1 – 2a2b2 – 2a3b3
But notice that
a12 + a22 + a32 = [(a12 + a22 + a32)0.5]2 = ||a||2
b12 + b22 + b32 = [(b12 + b22 + b32)0.5]2 = ||b||2
– 2a1b1 – 2a2b2 – 2a3b3 = -2(a1b1 + a2b2 + a3b3) = -2 (a ∙ b)
So
a12 + a22 + a32 + b12 + b22 + b32 – 2a1b1 – 2a2b2 – 2a3b3 = ||a||2 + ||b||2 – 2(a ∙ b).
The Cauchy-Schwarz Inequality
Though often used in linear algebra, this inequality is dependent on the definition of the dot product if it is to work at all. It states that |a∙ b| ≤ ||a|| ||b||, or that the absolute value of the dot product is less than or equal to the product of the magnitudes of a and b (789). Here is how we know this to be true.
First, we need to use one of the definitions of the dot product.
|a∙ b| = | ||a|| ||b|| Cos Θ |
Now we need to take a look at the possible values for Θ. When Θ = 0, Cos 0 = 1 so
|a∙ b| = | ||a|| ||b|| Cos 0 | = ||a|| ||b||
When Θ = 90, Cos 90 = 0 so
|a∙ b| = | ||a|| ||b|| Cos 90 | = 0.
Now, for the range 0 ≤ Θ ≤ 90, our cosine term is between zero and one, so the absolute value of the dot product is between zero and ||a|| ||b||. But what about the range of 90 ≤ Θ ≤ 180? Our cosine terms would be between zero and negative one, but because this is the absolute value of both sides, the net value is still the same as it would be for the 0 ≤ Θ ≤ 90 range. So from 0 to π the greatest |a∙ b| can be is
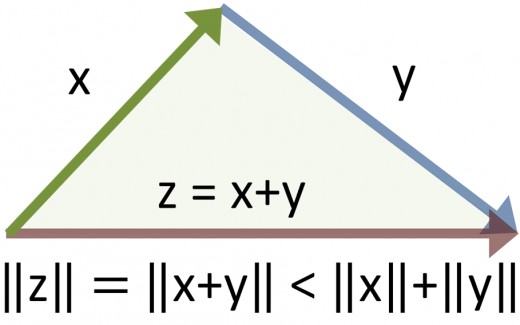
The Triangle Inequality
As the name implies, this identity stems from a triangle, specifically from the Law of Cosines. The actually inequality is ||a + b|| ≤ ||a|| + ||b||, or that the magnitude of the vector sum a + b is less than or equal to the actual sum of the magnitudes of a and b (789). Now, for the proof. The Law of Cosines states that
c2 = a2 + b2 – 2abCosΘ
Or that the long side of a triangle squared will equal the squares of both sides minus two times the sides and cosine of the angle opposite the long side of the triangle. If we make a triangle with short sides of ||a|| and ||b|| with a long side of ||a + b|| then we will have
||a + b||2 = ||a||2 + ||b||2- 2 ||a|| ||b|| CosΘ
Now, we will have several cases to examine. First, if Θ = 0, then Cos0 = 1 so
||a + b||2 = ||a||2 + ||b||2- 2 ||a|| ||b|| = (||a|| - ||b||)2
Or, after taking the square root of both sides,
||a + b|| = ||a|| - ||b||
Which is definitely less than ||a|| + ||b||, as the inequality states.
Now, what if Θ = 90? Then Cos90 = 0 so
||a + b||2 = ||a||2 + ||b||2
Which is not only the Pythagorean Theorem but it is also less than ||a||2 + ||b||2 + 2 ||a|| ||b||, or
||a + b||2 < ||a||2 + ||b||2 + 2 ||a|| ||b|| = (||a|| + ||b||)2
And after taking the square root of both sides, we have
||a + b|| < ||a|| + ||b||.
Just as we expect if the Triangle Inequality is true.
If Θ = 180 (which it couldn’t if this were a triangle), Cos180 = -1 so
||a + b||2 = ||a||2 + ||b||2- 2 ||a|| ||b|| (-1) = ||a||2 + ||b||2+ 2 ||a|| ||b|| = (||a|| + ||b||)2
Or after taking the square root of both sides
||a + b|| = ||a|| + ||b||
Again, a result that the Triangle Inequality states is possible. It is interesting to point out what this would look like. In this case, a and b would both be pointing in opposite directions, so the length of a + b would have to be the lengths of a and b individually.
So are we done with the proof? Not quite. What about for the theta range 0 ≤ Θ ≤ 90? That means that 1 ≤ CosΘ ≤ 0 and that everything on the right hand of the Law of Cosines is going to be greater than ||a|| - ||b|| but less than ||a||2 + ||b||2, which we know from both cases will be bigger than ||a + b||. We can use a similar argument for the range 90 ≤ Θ ≤ 180.
The Cross Product of the Cross Product
As the title implies, we will explore what the cross-cross product is. Below is the proof that will show that a x (b x c) = (a ∙ c)b - (a ∙ b)c (797). Note that
a x (b x c) = a x [i(b2c3 – b3c2) - j(b1c3 – b3c1) + k(b1c2 – b2c1)]
Which, if I write it in determinant form is
| i j k |
= | a1 a2 a3 |
| b2c3 – b3c2 -b1c3 + b3c1 b1c2 – b2c1 |
And that can be rewritten after taking the determinant as
i[a2(b1c2 – b2c1) – a3(-b1c3 + b3c1)] – j[a1(b1c2 – b2c1) – a3(b2c3 – b3c2)] + z[a1(-b1c3 + b3c1) - a2(b2c3 – b3c2)]
Oh boy, ready for this algebra?
i[a2b1c2 – a2b2c1 + a3b1c3 –a3b3c1] – j[a1b1c2 – a1b2c1 – a3b2c3 + a3b3c2] + z[-a1b1c3 + a1b3c1 - a2b2c3 + a2b3c2]
= i[a2b1c2 + a3b1c3 – a2b2c1–a3b3c1] – j[– a1b2c1 – a3b2c3 + a3b3c2 + a1b1c2] + z[a1b3c1 + a2b3c2 - a1b1c3 - a2b2c3]
And after distributing negative signs and distributing unit vectors we have
i[a2b1c2 + a3b1c3] –i[ a2b2c1 + a3b3c1] + j[a1b2c1 + a3b2c3] - j[a3b3c2 + a1b1c2] + z[a1b3c1 + a2b3c2] – z[a1b1c3 + a2b2c3]
And If I pull out select b and c terms we will have
ib1[a2c2 + a3c3] –ic1[a2b2+ a3b3] + jb2[a1c1 + a3c3] - jc2[a3b3 + a1b1] + zb3[a1c1 + a2c2] – zc3[a1b1 + a2b2]
= ib1[a2c2 + a3c3] + jb2[a1c1 + a3c3] + zb3[a1c1 + a2c2] –ic1[a2b2+ a3b3] - jc2[a3b3 + a1b1]– zc3[a1b1 + a2b2]
Now, if I add and subtract specific ab and ac terms so the sum of them is zero, I will have
ib1[a1c1+ a2c2 + a3c3 - a1c1] + jb2[a1c1 + a2c2 + a3c3 - a2c2] + zb3[a1c1 + a2c2 + a3c3 - a3c3] –ic1[a1b1 + a2b2 + a3b3 - a1b1] - jc2[a1b1 + a2b2 + a3b3 - a2b2]– zc3[a1b1 + a2b2 + a3b3 - a3b3]
But notice now that we have dot products! Further simplifying this now is
ib1[a ∙ c- a1c1] + jb2[a ∙ c- a2c2] + zb3[a ∙ c- a3c3] – ic1[a ∙ b - a1b1] - jc2[a ∙ b - a2b2]– zc3[a ∙ b - a3b3]
And after further distributing the terms, we have
ib1[a ∙ c]- ib1a1c1 + jb2[a ∙ c]- jb2a2c2 + zb3[a ∙ c]- zb3a3c3 – ic1[a ∙ b] + ic1a1b1 - jc2[a ∙ b] + jc2a2b2 – zc3[a ∙ b] + zc3a3b3
Notice how we have abc terms cancel out, so after eliminating those we have
ib1[a ∙ c] + jb2[a ∙ c]+ zb3[a ∙ c] – ic1[a ∙ b] - jc2[a ∙ b] – zc3[a ∙ b]
= [a ∙ c][ib1+ jb2+ zb3] – [a ∙ b][ic1 + jc2 + zc3]
= (a ∙ c)b - (a ∙ b)c
Works Cited
Larson, Ron, Robert Hostetler, and Bruce H. Edwards. Calculus: Early Transcendental Functions. Maidenhead: McGraw-Hill Education, 2007. Print. 772, 789, 797.
- Cross Product of Vectors Properties and Proofs
With the use of the cross product, vector calculus really takes off, exploring new ideas and concepts that would otherwise be denied to us. - Dot Product Properties and Proofs
The mysterious dot product has a basis in vector theory that has wide applications. Here we examine how we know what it is and how to use it.
© 2014 Leonard Kelley