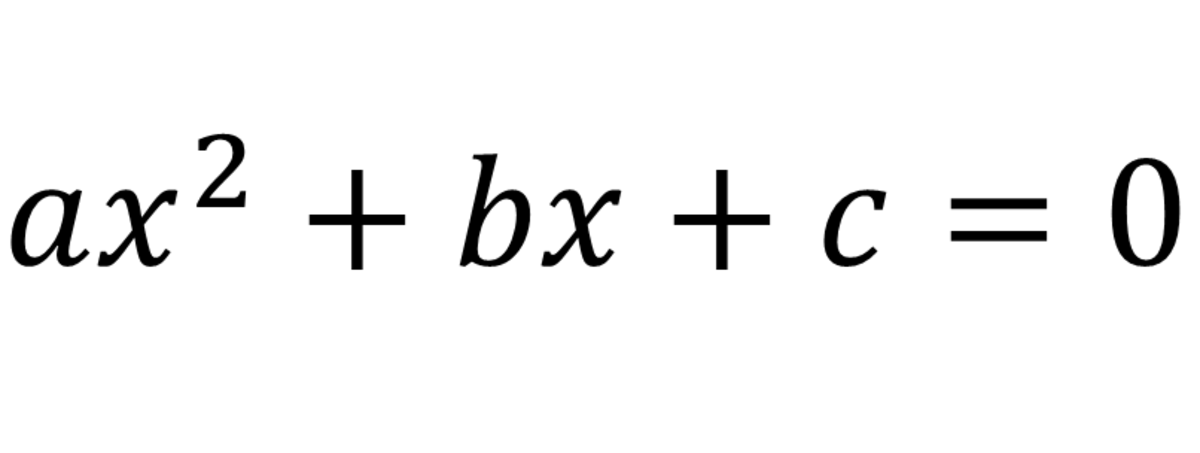Algebra: Completing the Square to Solve Quadratic Equations
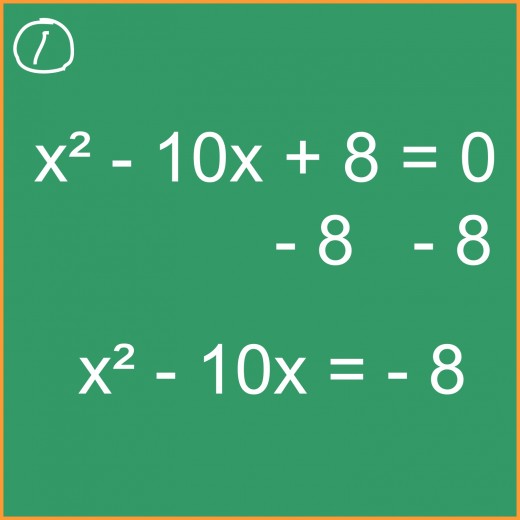
Step #1
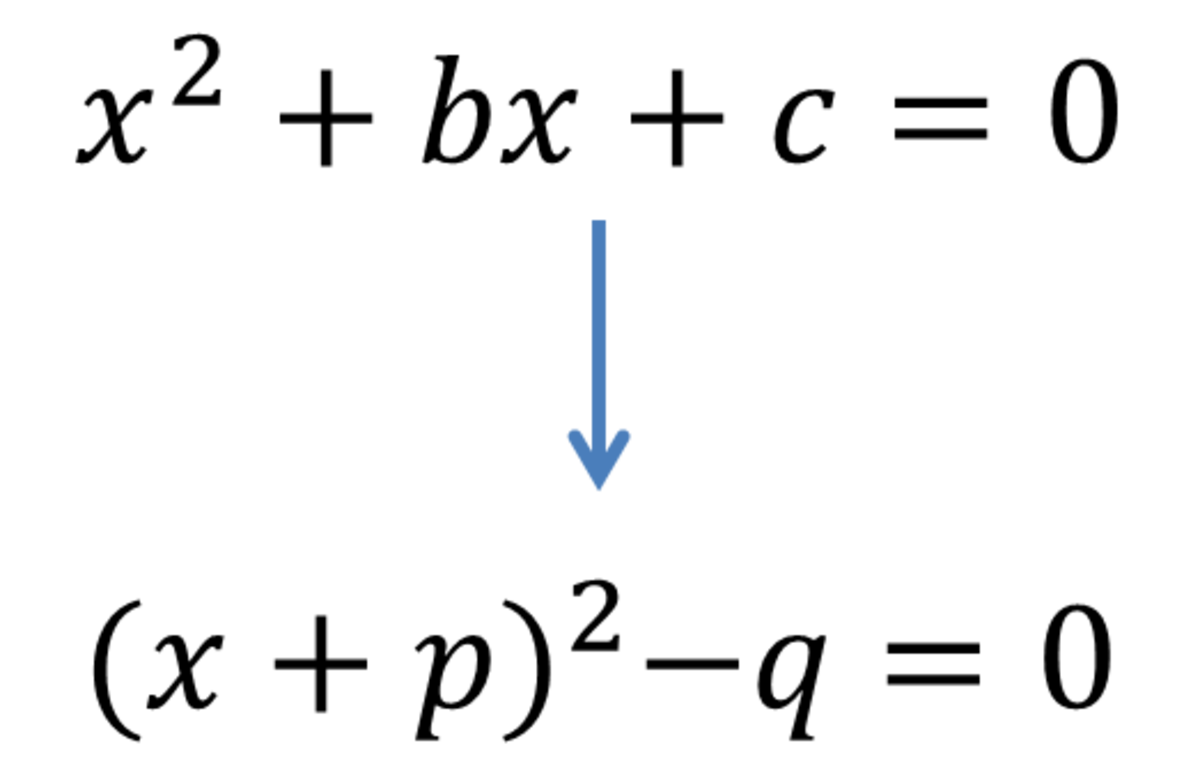
Considering the quadratic equation above (in the form ax2+ bx + c = 0), we see that the middle number (b) is -10, which can be represented as the sum of two identical numbers: (-5) + (-5). This is important because they will also double as the root of a square later on (the product of two identical numbers). So, we can now proceed to use the “completing the square” method to solve. Our first step is to isolate what will become our square by moving 8 (c) to the other side as shown in illustration #1.
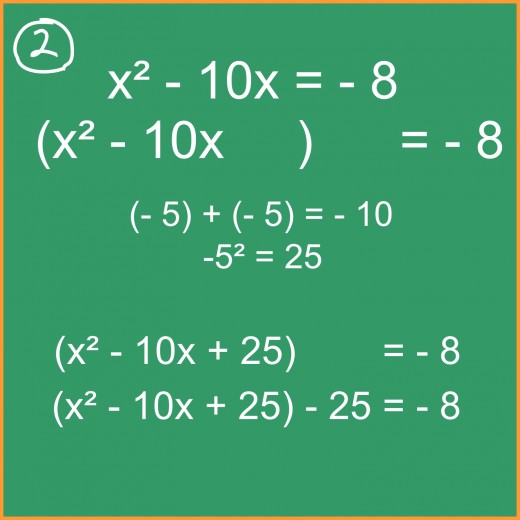
Step #2
We now need to find our new (c) number in the equation, which will now become a square. We already established that (-5) + (-5) = 10, and now we will use the product as our third number (c), which needs to be a square. In this case, it becomes 25. However, we are not done yet! After adding 25 to our square equation, we need to balance it out by also subtracting 25 outside of it. This is shown in illustration #2.
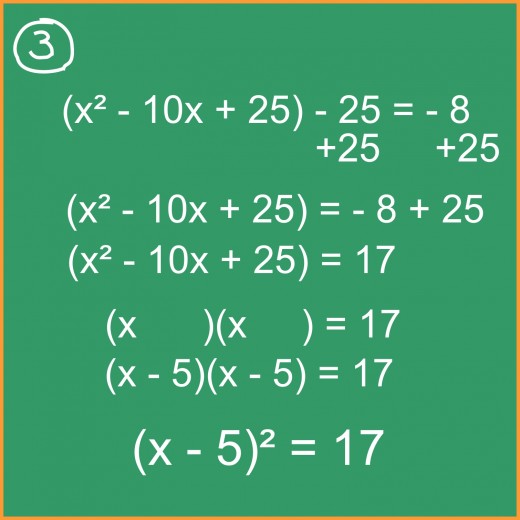
Step #3
Let’s now isolate the square equation by moving -25 to the other side via addition, where +25 combined with -8 becomes 17. Focusing then on our new square equation, we need to create the root. Split the equation into a pair of parentheses as shown. Remember our -5 from the beginning? Since it is the number (factor) that multiplies to become 25 (c) and adds to become -10 (b), we now fill it into the root as shown in illustration #3.
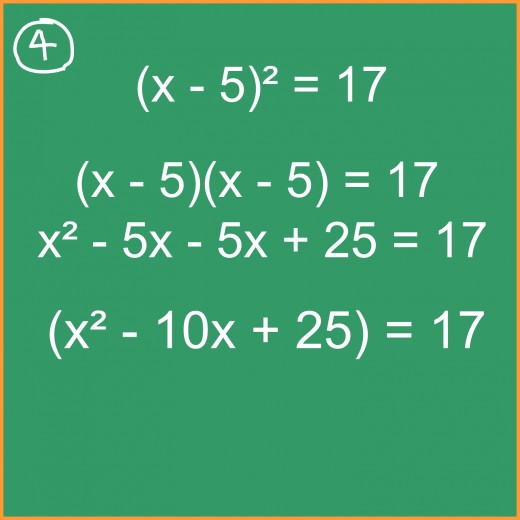
Step #4
Step #4
To prove this is the correct root, we can check it by solving using the FOIL method (multiply the first numbers, then the outside numbers, then the inside numbers, and then the last numbers) as shown in illustration #4. We see that we get our original square equation.
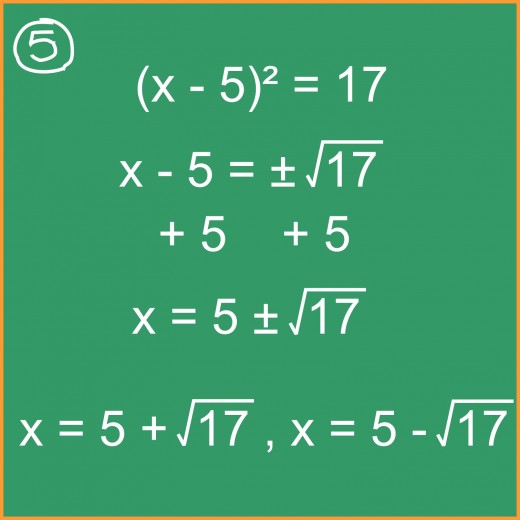
Step #5
Returning to the process, we now take the square root of both sides as shown in illustration #5 so that we are left with simply x – 5 on the left (and remember that the square root on the right will be + or -). Then, isolate x by moving 5 to the opposite side via addition. We now have our two possible solutions for x: 5 plus the square root of 17 and 5 minus the square root of 17.