An Easy Math Trick to Mentally Square Numbers Ending 5
Square of 5

What is a Square?
A square when referring to number in math comes from the geometric term square.
The square of 2 or a square with sides of 2. Is 2 to the power of 2 or 2 x 2 or 4
There are several way of notating a square
2^2 would notate the square
2 x 2 is a number sentence that represents the square.
A square of 5 would look like the images to the right side of the screen.
Imagine that you have a square with sides of 5. A squares sides are all the same so you would only have to notate the single 5 on one side. In order to find the area you would have multiply 5 by 5 or find the square of 5.
There are many tricks and patterns throughout math. This easy trick will help you do mental math for the squares of numbers ending in the digit 5 for all numbers that are greater than 5.
Squaring Numbers Ending in 5
There are many tricks to multiplying and squaring numbers.
This ones is easier than is looks.
Lets Start with what we know. We know the 5 squared or 5 times 5 is 25. This is a simple basic fact that you should already have memorized. If you don't know your basic facts, learn them! This is one thing I feel strongly about in math, if you don't know your facts math will always remain hard and out of reach.
This trick will work for every one after 5.
15, 25, 35, 45, 55, and so on.
Let us look at the first example.
Finding the Square of 35
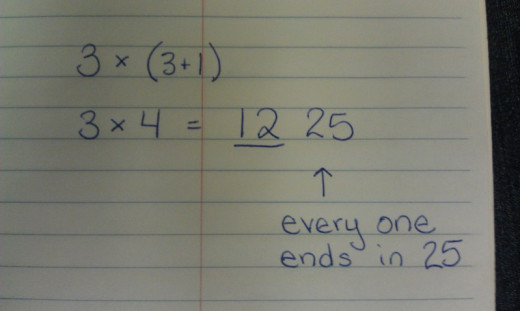
Finding the square of 35
The first example is of the number 35.
The three is the digit we need to find the square. The five is going to be ignored. We already know 5 times 5 is 25 so all the numbers will be ending in the number 25. We are going to tack these digits onto the back end of the digits that this trick finds.
We need the digits in front of the 5 in order to make the trick work.
The digit(s) in front of the 5 for this problem is 3.
We need 3 and one more than 3.
We are going to multiply 3 by (3 +1)
3 x 4 =12
Then we tack 25 onto the end
to get 1225.
The square of 35 is 1225.
The square of 75
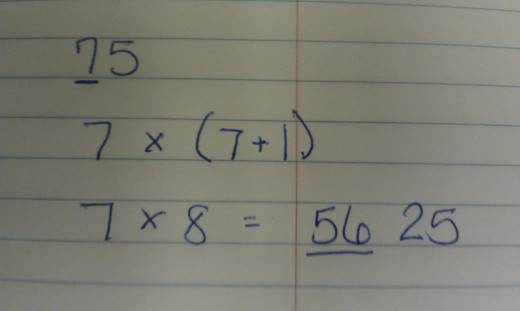
Square of 75
The same concept applies here
The digits before the 5 is 7. We need 7 and 1 more than 7.
7 times 8 equals 56.
56 tack on 25
5625.
One final example of Squaring a 5 Number
Just to make sure this pattern continues we are going to try a multi digit numbers and calculate the same thing.
135 is the number I am going to use for this.
I am using this number because it has more than one digit in front of the 5 to show that this pattern continues to work.
Example of the Square
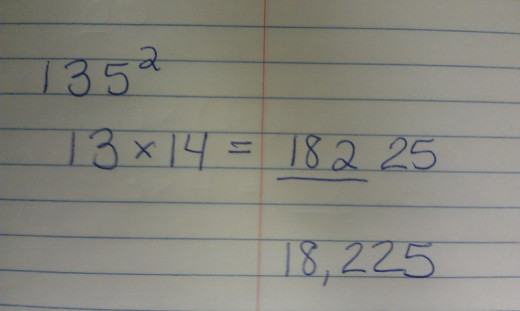
Patterns in Math
If you write out the squares you will see something like this:
25
225
625
1225
2025
3035
4225
5625
7225
and so on.
See if you can find the patterns in other squares that will help you be faster and more effective in math.