An Introduction to Quantum Computing

• What Quantum Computers are all about
• How Quantum Computers Work
• Classical Bit and Functions on Classical Bit
• Quantum Bit
• Superposition, Entanglement and Teleportation
• What Quantum Computers Cannot Do
• Conclusion

Following are few things that I am assuming that you already know or at least have seen them.

• Complex Numbers: Basic definition, Conjugates
• Matrices: Matrix multiplication, Addition
• Vectors: As in column matrices
• Linear Algebra: Specifically, Basis vectors and their linear combinations

That's all you need to know to get most out of this article.

Quantum Computer is a new kind of computer based upon Quantum Mechanical properties of subatomic particles. Unlike computers, we have today, which work by controlling the flow of electricity inside transistors, Quantum Computer manipulate subatomic particles and their spins (I will explain this further).

The main advantage that quantum computer has against classical computer is that It can keep track of lots of things at once and perform calculations on them without getting blogged for example It can simulate a complex protein chain which can make even the fastest supercomputer that we have today shy. This property even let them break one of the most resilient cryptosystem that we have today in matter of minutes.

Quantum Computers are fairly complicated machines. They require sophisticated cooling equipments for working and also an environment that is completely barred from external disturbances such as electromagnetic radiation.

The basic unit of information in quantum computers is Qubit. A qubit is mathematically represented as 2-dimensional vector (a 2D Array) in complex vector space called Hilbert Space. What this means is that we use complex numbers or 2-dimensional numbers in quantum computing.

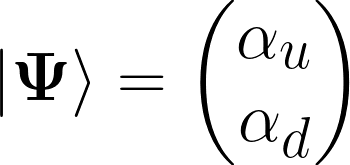
|Ψ> is used to represent a vector in Hilbert Space. The notation used here is called Bra-Ket notation which is used throughout quantum physics to work with vectors in Hilbert space. α_u and α _d represent two complex numbers Up and Down.

These complex numbers Up and Down are of special importance to us because they represent Spins. While we are measuring a Qubit (that is observing the value of qubit) we compute magnitude of these two complex numbers by performing their squaring α²_u and α²_d. Whichever quantity is bigger the Qubit collapses to that side for example if α_u > α_d then qubit is said to have collapsed to Up state.

One important constraint that must be satisfied by α_u and α _d is that the sum of their squares should be equal to 1. Because a quantum bit can either be in Up or in Down state. If it is in Up then probability of it being Down becomes 0 thus states Up and Down are mutually exclusive.

All this discussion must have tinged the light bulb inside your brain that Qubit behaves just like a classical bit (the one used by all the digital computers) and you would be partially right. However, quantum bit holds much more information than their classical counterpart as you will see in upcoming sections.

Classical computer use classical bit as unit of information. A bit can have two possible states either 1 or 0. We can represent these states with 2-dimensional vectors. Where a 1 in first place indicates bit is in off(0) state and 1 in second place indicates bit is in on(1) state. Note that a vector having 1 at both positions will cease to be valid.

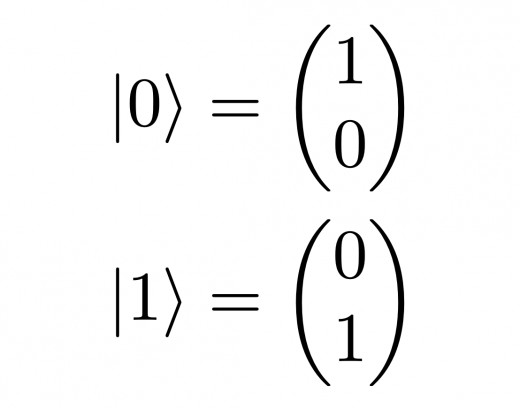
Let us also define all the one bit functions in the form of matrices which on multiplication with bit vectors perform the function on bit. Four single bit function are:

1. Not
2. Identity
3. Constant-0
4. Constant-1

Note that multiplication here means matrix-dot multiplication which is different from multiplication we do with real numbers. You can read more about it here.

Here how a Not function (commonly not gate) on bit vector can be applied. Recall that Not gate has property of negating the input. Given 0 it outputs a 1 and vice-versa.

Till now, we have seen how classical bits can be defined in terms of vectors and how we can perform or apply basic functions on them using matrix multiplication. Next question is how do we go from classical bit to quantum bit?

Quantum Bit as I've said earlier is representation of quantum state. And quantum states are represented as vectors in Hilbert space which have complex values at every point. Hence, the only difference between quantum bit and classical bit is we throw in complex numbers which tells probability amplitudes of bit coinciding with particular configuration either 0 or 1.

Thus, Quantum bit is lot more powerful and interesting than classical bit. For example, following equation represents qubit Ψ as sum of two vectors U and D again α's represent individual probability amplitudes of being Up and Down. This simply means unless and until we go around measuring the qubit; It can be in an infinite number of states. If you know Linear Algebra then this is same as saying that U and D are basis vectors in Hilbert space and unless we go and see for ourselves the quantum bit can be any of one of the linear combinations of these two vectors.

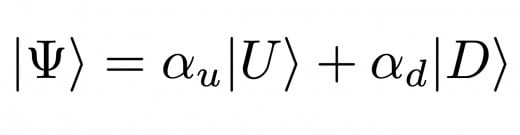
The verdict of this is Quantum Bit can represent multiple classical bits and hence quantum computer working on them can process a lot more information than classical computer.

Think that's all? Well, not quite yet; Quantum computing has few more rabbits yet to come out of the hat. Three to be specific:

• Superposition
• Entanglement
• Teleportation

Superposition is what Schrödinger's cat is all about. When we put a Qubit in superposition state (by application of Hadamard Gate, will see in next article) then qubit can either be both in Up state or in Down state(i.e. they have equal probability amplitudes).

Superposition is powerful. In fact, most of the quantum algorithms work by first placing qubits in superposition states and then start the actual work after application at the very end, they reapply Hadmard Gate to put qubits back into normal state and get them ready for measurement.

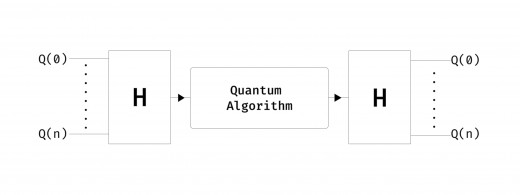
Mathematically it is represented by setting probabilities amplitudes to 1/√2 so that on squaring the probabilities become 1/2 which indicates that both spins has 50-50 chance of occurring just like a coin flip.

Superposition is so important that it deserves an individual article and It surely will get in time soon.

Last, but not the least, Two of the most controversial consequence are quantum entanglement and teleportation. Quantum Entanglement is when two qubit decide to get along together so much that even distance of light years doesn't matter.

Imagine that there is a light source continuously giving out photons of different polarizations. Now imagine two detectors on opposite sides of this light source. As we know light is polarized either in x-direction or in y-direction. But, our detectors only detect photons polarized along x-direction. When right photon is detected, they glow and remain dark otherwise.

Let's turn the source of light on and observe things as they are occurring. When entanglement is at play, moment a mutually entangled pair of photons leaves the light source in opposite directions, interesting thing happen, If one of the photons gets detected the another one on opposite side gets detected too. If one of the photons doesn't get detected then another one will also get ignored by the detector.

I know, you might be thinking how can two photons decide just moments before colliding with detector whether they want to get detected or not this might seem complete nonsense to you but mind you, this has been tried and tested countless times as this was the original experiment performed to detect entanglement and every time entanglement was observed.

Entanglement works even when two quantum systems are light year away from each other, the moment one is decided (or measured) another one gets concluded too. How weird or powerful it might sound, Quantum entanglement still cannot be used to transfer data or quantum object in instant because that would break law of relativity as it would have travelled faster than light and no signal can travel faster than light. But we want to send information right? This is where Quantum Teleportation comes in.

Quantum Teleportation is transfer of information and quantum state between an entangled pair of qubits called EPR pair. Well I, will explain this one further too in upcoming article where we will implement and run quantum algorithms taking advantage of these three (Superposition, Entanglement and Teleportation) that will make things much more clearly.

Of course Quantum Computers are not here to replace classical computers. Classical computers will continue to do what they are currently doing for decades to come.

Quantum computing will, however, most certainly replace classical computing in Artificial Intelligence, Cryptography, Communication and Simulation. In general wherever there is need for computing many distinct possible outcomes and choosing one. Sadly, you won't see latest, greatest game title with life like graphics running on a quantum computer (It would run slower than it otherwise would have on classical computer).

Quantum computer are fun. Even Schrödinger's cat is proud of its enormous power. In this article I've barely scratched the surface of an ice-berg. There's lot to be learned and understand which I cannot possibly fit in 1230 words or so article. But worry not, I will try my best. In upcoming articles I will write about tensors, tensors product for representing multiple quantum bits and various quantum gates. Until then, Have a nice one and Don't forget to ask questions or point out mistakes. Happy Learning!