Opposite Angles In A Cyclic Quadrilateral Add Up To 180 Degrees. Circle Thoerem Examples.

A cyclic quadrilateral is basically a 4 sided shape that is drawn inside a circle. All four vertices of the quadrilateral must lie on the circumference of the circle. In a normal quadrilateral the angles will add up to 360 degrees, but if you have a cyclic quadrilateral then the opposite angles will also add up to 180 degrees. Therefore, the circle theorem for this cyclic quadrilateral is:

Opposite angles in a cyclic quadrilateral add up to 180⁰.

Let’s take a look at some examples which involve using this circle theorem.

Example 1

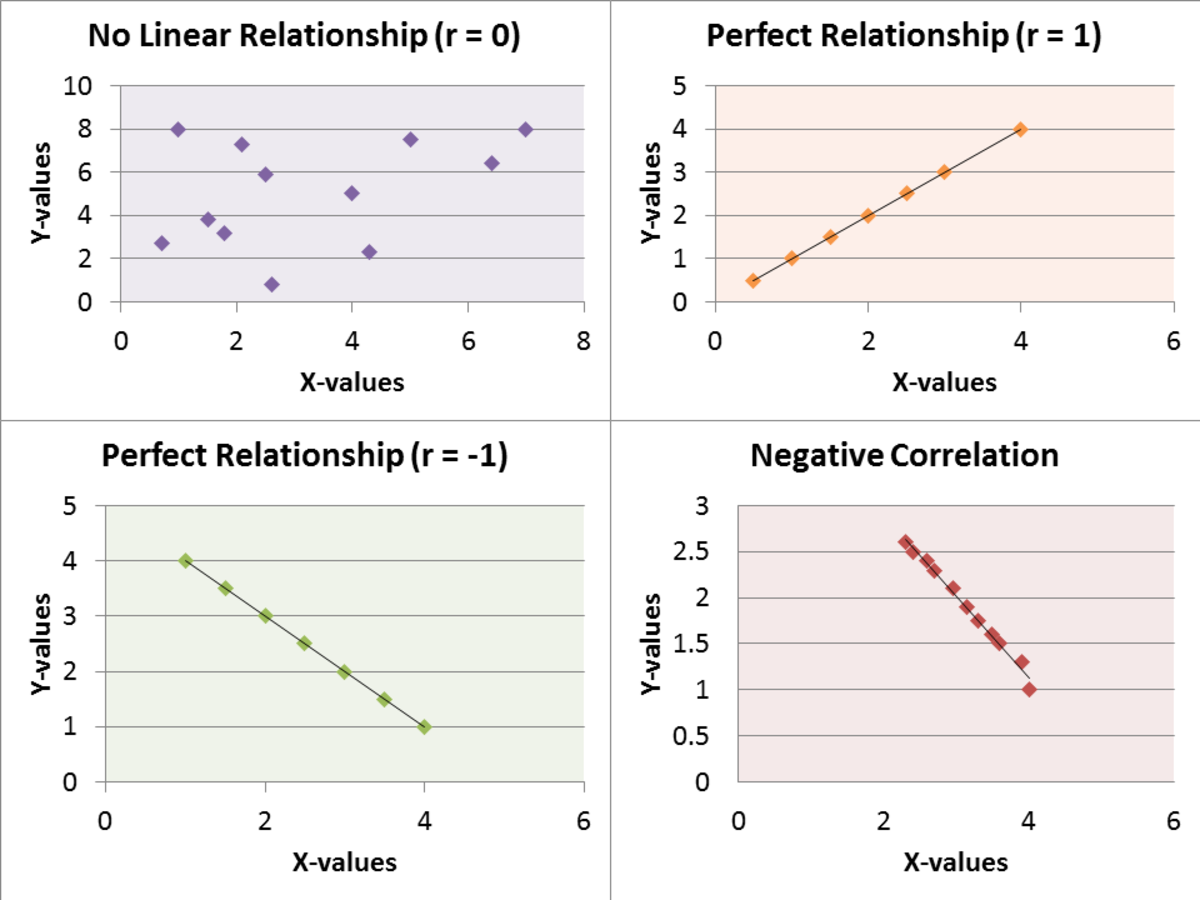
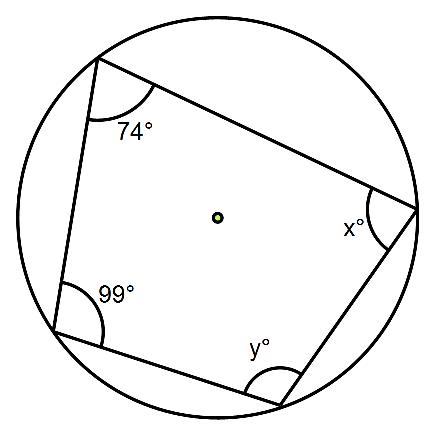
Work out the size of angles x and y in this cyclic quadrilateral.

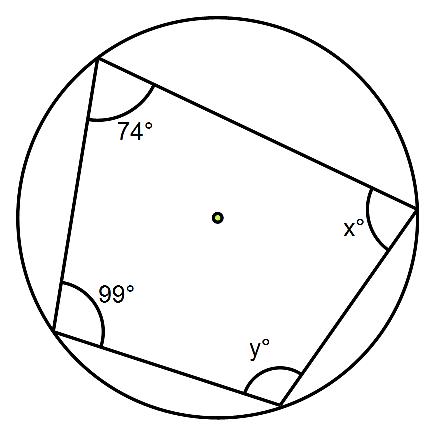
All you need to do is use the circle theorem above, opposite angles in a cyclic quadrilateral add up to 180⁰.

Let’s begin by working out angle x.

The angle opposite angle x is 99⁰, so x + 99 = 180⁰. So to find x just subtract 99 from 180 to give 81⁰

Let’s now work out angle y.

The angle opposite angle y is 74, so y + 74 = 180⁰. So to find y just subtract 74 from 180 to give 106⁰.

So angle x is 81⁰ and angle y is 106⁰.

As a final step, you can check that these angles correct by finding the total of the four angles. All four angles should add up to 360⁰. So let’s check that these four angles add up to 360:

99 + 81 + 74 + 106 = 360⁰.

Since the total of all the angles is 360⁰ then angles x and y must be correct.

Example 2

Work out the size of angles c and d in this cyclic quadrilateral.

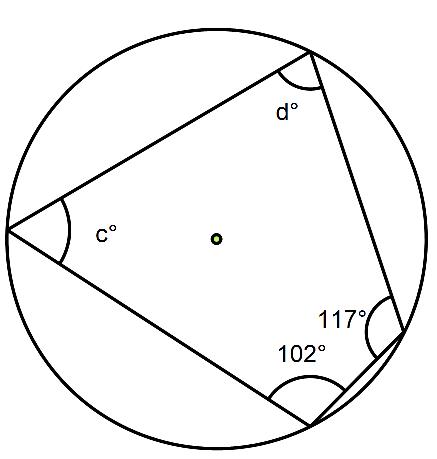
All you need to do is use the circle theorem above, opposite angles in a cyclic quadrilateral add up to 180⁰.

Let’s begin by working out angle c.

The angle opposite angle c is 117⁰, so c + 117 = 180⁰. So to find c just subtract 117 from 180 to give 63⁰

Let’s now work out angle d.

The angle opposite angle d is 102, so d + 102 = 180⁰. So to find d just subtract 102 from 180 to give 78⁰.

So angle c is 63⁰ and angle d is 78⁰.

Like example 1, you can check that these angles correct by finding the total of the four angles. All four angles should add up to 360⁰. So let’s check that these four angles add up to 360:

117 + 63 + 102 + 78 = 360⁰.

Since the total of all the angles is 360⁰ then angles c and d must be correct.

For some harder example on using this circle theorem check out this page:

Circle Theorem Help. Extra Examples On Opposite Angles In A Cyclic Quadrilateral Total 180 Degrees.