Atomic Orbitals
Quantum Mechanical Description of Electrons in Atoms
Bohr’s concept of well-defined orbits for electrons is no longer acceptable, because it is inconsistent with Heisenberg's Uncertainty Principle. However, the idea of energy quantization that Bohr introduced is still accepted today. We just have a different way of determining what the allowed energy levels are.
Modern Quantum Theory proposes a probabilistic model for atoms. One of the postulates of modern quantum theory is that anything we want to know about an atom or molecule can be obtained from a mathematical function, which is customarily represented by the Greek letter psi (Ψ). This, of course, assumes that Mother Nature gives us access to this information. For example, we cannot precisely determine location and velocity of an electron simultaneously; this information is not accessible according to the Heisenberg uuncertainty principle.
The mathematical function that provides us with all accessible information about a particle is called a wavefunction, and it is determined by solving what is known as the Schrodinger equation. An orbital is a wavefunction that allows us to describe the probabilities of locating an electron at any given location. From the probabilities, we can calculate such things the average distance of an electron from the nucleus and the most probable distance. An orbital also gives us information about the energy of an electron, the energy needed to remove it from the atom (ionization energy), and the magnetism resulting from its motion around the nucleus.
Exercise: Atomic orbitals are mathematical functions that allow us to determine all of the following except...
A. the location and velocity of an electron at any given time,
B. the probability of finding an electron in any given region,
C. how an atom would behave in a magnetic field,
D. the energy needed to remove an electron from an atom
Answer:
Visualizing Atomic Orbitals
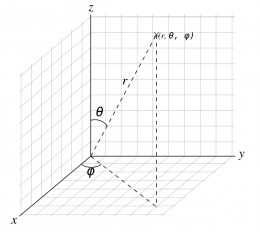
An atomic orbital is a mathematical function that depends on the location of an electron. As a matter of convenience the nucleus is defined as the origin and locations are expressed using spherical polar coordinates (r, θ, Φ) as shown in right photo . The coordinate r is the distance from the nucleus; θ (theta) and Φ (phi) are called directional angles.
The spherical polar coordinates are related to Cartesian coordinates (x,y,z) as follows:
z = r cos(θ),
x = r sin(θ) cos(Φ),
y = r sin(θ) sin(Φ)
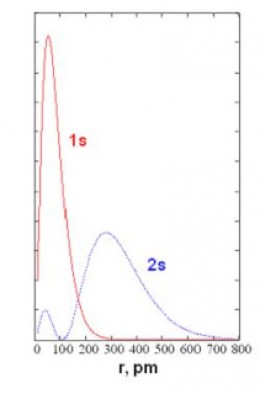
The Radial Distribution Functionassociated with an orbital describes how the probability of finding an electron varies vs. distance from the nucleus. Radial distribution functions for the "1s" and "2s" orbitals of hydrogen are shown in the graph below. The horizontal axis is r (distance from nucleus) in picometers (pm). The vertical axis is the relative probability. You can see that in the orbital called "1s," the most probable distance is 52.9 pm; the red curve peaks at r=52.9 pm. Bohr's "old quantum theory" predicted a stable electron orbit at 52.9 pm; modern quantum theory predicts 52.9 pm as the most probable distance for an electron described by the 1s orbital. The electron can actually be anywhere from very close to very far away from the nucleus.
Electron clouds or charge clouds are used to visually represent orbitals. The probability of finding an electron is higher in regions where the cloud is thicker.
A boundary surface is often drawn such that the probability of finding the electron (being described by the orbital) is low outside the surface. The algebraic sign (+ or -) of the function is oftentimes indicated, or color coded. The shape of the boundary surface resembles the shape of the electron cloud; it depends on how the orbital depends on the directional angles (theta and phi). The size of the surface depends on how the orbital depends on the distance from the nucleus (r).
Note that s orbitals are spherically symmetrical --- the orbital depends only on distance, not direction. The p orbitals can be described as consisting of two lobes.

Orbital Names and Quantum Numbers
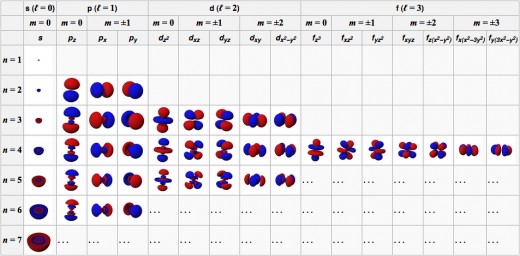
Shells and subshells
Each atom has a set of orbitals, which can be grouped into shells or levels. The shell or level number is called “n” or the “principal quantum number”
In the first shell (n=1), there is only one orbital. That orbital is called 1s.
In the second shell (n=2), there are four orbitals. One is called 2s, the other three are called 2p.
The 2s orbital is also called the 2s subshell or sublevel. The three 2p orbitals comprise what is called the 2p subshell. We could say that there are two types of orbitals in the second shell; each type comprises a subshell.
In the third shell (n=3), there are three subshells. One orbital is in the 3s subshell, three are in the 3p subshell, and five are in the 3d subshell. The total number of orbitals is 9: 1+3+5 = 9.
In any shell,
- the first subshell is always called "s" and consists of 1 orbital.
- the second subshell is always called "p" and consists of 3 orbitals.
- the third subshell is always called "d" and consists of 5 orbitals.
- the fourth subshell is always called "f" and consists of 7 orbitals.
- the fifth subshell is always called "g" and consists of 9 orbitals.
Do you see a pattern in the number of orbitals? It's 1, 3, 5, 7, etc. for subshell s, p, d, f, g, etc. After g, sublevel names are alphabetical; you are not likely to encounter any subshells beyond g.
In general, the nth shell has n subshells and n2 orbitals. Example: for n=5, there are 5 subshells, and 25 orbitals; 1+3+5+7+9 = 25.
An orbital's type (that is, the subshell it belongs to) is related to the orbital's shape. Orbitals in the s subshells (the "s orbitals") are spherically symmetrical; p orbitals can be described as having two lobes, etc.
An alternative way of referring to a subshell or orbital type is the orbital or azimuthal quantum number, which is often represented by lowercase ell in script (ℓ). The orbital quantum number is
- 0 for s orbitals,
- 1 for p orbitals,
- 2 for d orbitals,
- 3 for f orbitals,
- 4 for g orbitals, etc.
To summarize, the orbitals an atom are:
- For n=1: 1s
- For n=2: 2s, 2p (set of 3)
- For n=3: 3s, 3p (set of 3), 3d (set of 5)
- For n=4: 4s, 4p (set of 3), 4d (set of 5), 4f (set of 7)
etc. Note that for a given n, the allowed values of the orbital quantum number (ℓ) are zero up to (n-1). For example, the allowed values of ℓ for n=3 are 0, 1, and 2; these three ℓ values correspond to 3s, 3p, and 3d orbitals, respectively.
Exercise: Which of the following are allowed values of the quantum numbers n and ℓ, respectively ?
A. 1.5 and 0, B. 3 and 3, C. 2 and 1, D. 0 and 1
Answer:
Exercise: What is the value of the orbital quantum number for an electron in a 3p orbital?
A. 0, B. 1, C. 2, D. 3
Answer:
Exercise: Which of the following is not a valid name for an atomic orbital?
A. 1s, B. 2s, C. 2d, D. 3p
Answer:
Magnetic quantum number
All orbitals in a given subshell have the same principal and orbital quantum numbers ( n and ℓ). The magnetic quantum number, represented by the letter m or “em sub ell” (_{m _ℓ}), distinguishes orbitals within a subshell. Examples:
The p subshell consists of 3 orbitals. One orbital corresponds to _{m _ℓ}=-1; another orbital corresponds to _{m _ℓ}=0; and another orbital corresponds to _{m _ℓ}=+1.
For a d subshell, there are 5 orbitals and the possible _{m _ℓ} values are -2, -1, 0, 1, +2
In general, for a given subshell (ℓ), there are (2 ℓ + 1) possible _{m _ℓ} values: -ℓ to +ℓ.
Exercise: Which of the following is not an allowed value of the magnetic quantum number (_{m _ℓ ) for an electron in a 3d orbital? A. 3, B. 2, C. 0, D. -1
Answer:
Why is _{m _ℓ} called the magnetic quantum number? The motion of electron around the nucleus generates a magnetic field. Any type of curved motion of a charged particle generates a magnetic field. View the animation in the link below. Imagine the sphere is an electron: the green vertical arrow (that points up or down as the sphere moves) is called the “orbital angular momentum vector” and is pointing to the south pole of magnetic field generated by the motion of the electron.
Each _{m _ℓ} value corresponds to one allowed orientation of the magnetic field, except for electrons in s orbitals. For p orbital, imagine an invisible bar magnet inside the atom that is oriented in one of three ways.
In each of these,the actual North-South line of the magnet is not stationary. It is precessing around a cone of uncertainty centered the vertical axis. For more on the concept of precession, click here or watch above videos:
Exercise: How many ways can the magnetism generated by the orbital motion of an electron in a 3p orbital be oriented? A. 1, B. 3, C. 5, D. 7
Answer:
Electron Spin
The magnetic properties of atoms suggest that electrons have an intrinsic magnetism, in addition to the magnetism that is generated by their motion around the nucleus. By intrinsic, we mean that they are magnetic just by being electrons. Since magnetism is associated with a circular type of motion of a charged particle, it is useful to imagine the intrinsic magnetism of an electron as resulting from a spinning motion. Motion of an electron around the nucleus is analogous to a planet revolving around the sun, while electron spin is analogous to the rotation of the planet around its own axis. To be consistent with experimental results, we have to assume that the magnetism due to electron spin can be oriented in one of only two ways. You can visualize the two possibilities by imagining an invisible bar magnet which can be oriented.
An electron in these two possible cases are also referred to as having a spin quantum number ms of +1/2 (spin up) or –1/2 (spin down). An electron in an atom is completely described by specifying four quantum numbers (n, ℓ, _{m _ℓ}, ms). The quantum numbers n and ℓ tell us the shell and subshell; the quantum number m tells us which orbital; and ms tells us the spin.
Pauli’s Exclusion Principle: "no two electrons in an atom can have the same set of quantum numbers."
For a given orbital (n, ℓ, and _{m _ℓ},), there can be only two possible ms values… +1/2 and –1/2. Therefore, Pauli's principle can also be stated as: "the maximum number of electrons assigned to an orbital is two; if there are two, one must be “spin up” and the other “spin down.”
Example 1: How many electrons can be assigned to a 4p orbital? Answer: 2, for any orbital. Both electrons will have the same n, ℓ, and m quantum number: n=4, ℓ=1, and m can be +1, 0, or -1. But one electron has ms=+1/2, the other has ms=-1/2.
Example 2: How many electrons can be assigned to 4p orbitals? Answer: 6, since 4p orbitals come in sets of 3, and a maximum of 2 electrons can be assigned per orbital. All six will have n=4, ℓ=1. They differ in _{m _ℓ} and ms values; the six possible (_{m _ℓ}, ms) values are:
(1, 1/2), (0, 1/2), (-1, 1/2)
and
(1, -1/2), (0, -1/2), (-1, -1/2).
The first three are "spin up"; the other three are "spin down."
Example 3: How many electrons can be assigned to a 4p subshell? Answer: 6, since a 4p subshell consists of three 4p orbitals. Maximum occupancy is 2 electrons per orbital; 2x3=6.
Example 4: How many electrons can be assigned to the n=3 shell? Answer: 18.
In the n=3 shell, there are 3 subshells (3s, 3p, 3d).
- The 3s subshell consists of 1 orbital.
- The 3p subshell consists of 3 orbitals.
- The 3d subshell consists of 5 orbitals.
- The total number of orbitals is 1+3+5, or 9.
- Maximum occupancy is 2 electrons per orbital; 2 x 9 = 18
Exercise: How many ways can the intrinsic magnetism of an electron in a 4d orbital be oriented?
A. 2, B. 3, C. 5, D. 10
Answer:
Exercise: What is the maximum number of electrons that can be assigned to a 2p orbital of an atom?
A. 2, B. 3, C. 6, D. 10
Answer:
Exercise: How many sets of quantum numbers can an electron in a 4p subshell have?
A. 2, B. 3, C. 6, D. 10
Answer:
Exercise: Which of the following can accommodate the most number of electrons?
A. a 4f orbital, B. the 3d subshell, C. the n=2 shell, D. a 3d orbital
Answer: