Basics of a Topological Space: What it all Means

When I took my first course in topology, I struggled. Topology was the most abstract mathematics I had encountered, and my problems started at the very beginning, with something I did not grasp until much later, namely: what is a topological space?

A topological space has to components: first, a set we might call X. This set can consist of just four components, like {a,b,c,d}, or it can be all numbers on the real line.

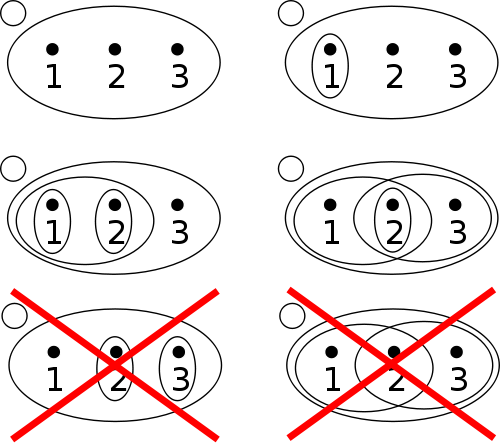
The second part is what we often call the topology on X, which we may denote by T. This consists of a series of subsets of X, a subset being a collection of the points in X, which satisfy these four conditions:

1) The empty set is in T.

2)X is in T.

3)The intersection of a finite number of sets in T is also in T.

4)The union of an arbitrary number of sets in T is also in T.

This was relatively easy to understand, what was harder was to comprehend the significance of T. A random series of subsets, but they are treated with such importance? Theorems I read seemed to signify that the exact contents of T were of massive importance.

Well, here is the important part: T is not a collection of open subsets, it is the collection of all open subsets in this topological space. So if we let X be the real line(or more spesifically, all point on the real line), and T1 be the collection of all open sets (a,b) where a and be are any real numbers and a<b, and their unions, you will have the normal number line that you know from other mathematics. You can get an open interval from any two numbers, that ends just between them.

However, let X again be the real line, and this time, let T2 be the sets (a,b), where a<0 and b>0, and their unions. This space works quite differently, as any open interval contains 0. All intervals from 2 to 3 contains 0, in fact, meaning that you can never find a neighborhood(made of open sets) around 2 that does not contain 0. No matter how tiny you try to make the interval, 0 is always there. This means that (X,T) is not Haussdorff for example, its properties have changed radically.

Another important implication of changing your topology on X, is that continuity of functions change. As you may know, a function f from A to B is continuous if and only if any open set in B will go to an open set when the inverse of f is being applied. Note that this does not mean that any open set in A must be sent to an open set in B.

Now, if we let f go from (X,T1) to (X, T2) by letting any any point be sent to itself(since they contain the exact same points), then f is continuous. After all, all open sets (a,b) where a is smaller than 0 and b is larger, fulfills the requirement of a and b being real numbers, which is the only requirement in T1.

But look at g, which we say is the inverse of f, going from (X, T2) to (X, T1). This function is not continuous, as for example the open set in (2,4) in T1 is not open in (X, T2), as 0 is not in it. So the topological space is decisive in continuity. From this it also follows that what T contains is essential when it comes to path-connectedness and connectedness.

Or let X be the set {a,b,c,d}, and T be the empty set, X, and the open sets {c}, {a,b} and {a,b,c}. What are the closed sets here? The definition of a closed set is the complement of an open set, so the complement to A is X-A. The closed sets here are {a,b,d}, {c,d} and {d}, pluss the empty set and X itself, being complements of each other. Then we have the closure of A, which is the smallest closed set that contains A. This can be found by taking the intersection of of all closed sets which contains A. Let A be {c}, and the closed sets with c in it are {c,d} and X. The closure of {c} is {c,d}. If you take {d}, which is closed, you will find its closure to be itself, {d}, as you would expect. The closure of {a}, which is neither open nor closed, is {a,b,d}.

As I said, when I first took topology I struggled with understanding what the topology on X really changed, and I write this with the hopes of other people not having to go through the same. While X provides the set of points, T gives us the structure between them, and how they are connected. This is why so many of the terms and theorems in topology focuses on the topological space. Changing the topology is how you make a topological space truly different from what you encounter in analysis or with complex numbers, both of which are just a couple of examples of topological spaces themselves.