The Bohr Model

The Problem with the Nuclear Model of the Atom
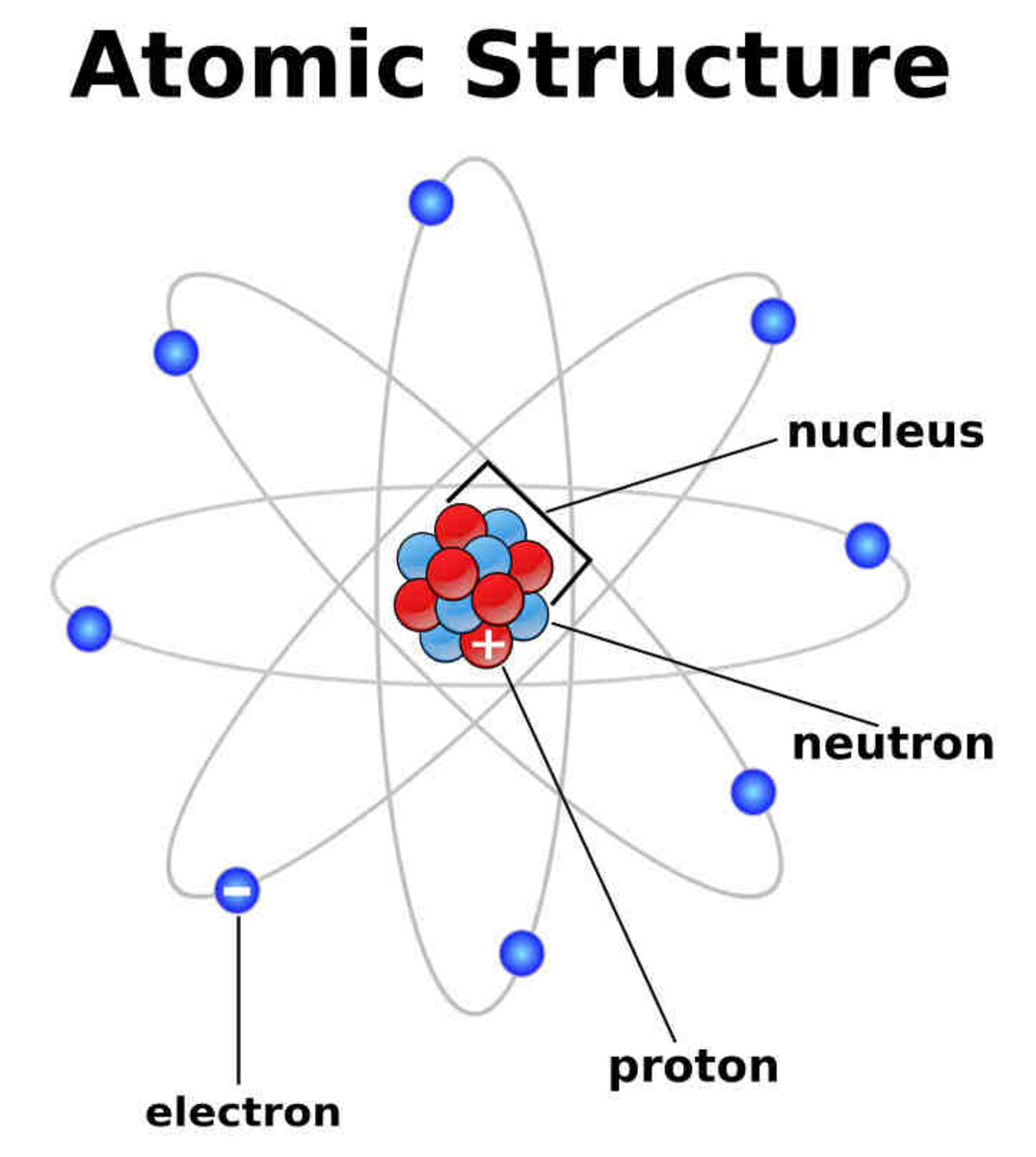
The currently accepted model of the atom is called the nuclear model and is based on the results of Rutherford's alpha scattering experiments. In this model, most of the mass of the atom is concentrated in a very tiny (10-13 - 10-14 m in diameter) positively-charged nucleus. The space occupied by the nucleus is very, very small compared to the rest of the atom, where negatively-charged electrons are found. The region around the nucleus is mostly empty space as the electrons, themselves, are much much smaller in mass and size compared to the nucleus. Initially, it was thought that electrons revolve around the nucleus like planets moving around the sun; this idea is no longer accepted. The problem with the nuclear model was that, based on what was known at that time, such a structure would be very unstable and should not last long enough to be observed. Actually, none of us would even exist and be able to observe anything since we're made of atoms, too. It is known that a charged particle, such as an electron, will emit electromagnetic radiation if it is accelerating. Something is said to be accelerating if it is not moving at constant speed in a straight line. Therefore an electron moving around a nucleus is accelerating and will continually emit electromagnetic radiation and lose energy. It should not take very long for the electron to crash into the nucleus.
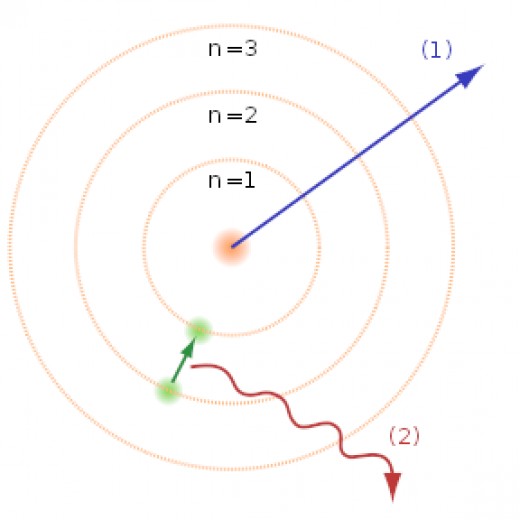
The Bohr Model
Niels Bohr made a bold suggestion that a nuclear atom can be stable in certain cases. Bohr assumed that some circular orbits are allowed. The derivation of the allowed orbits and the energy of the electron, for hydrogen and ions with only one electron, can be found at Here.
Allowed orbits
Based on his assumptions, a stable hydrogen atom is one where the electron can only be in circular orbits with a radius of r = (52.9 pm)(n2), where n=1, 2, 3, ...Note: 1 pm = 10-12 m. The radius of the first orbit, 52.9 pm, is called the Bohr radius and is often represented by the symbol a or ao. Therefore, r = a n2
The "Bohr" is also used as a unit of length; 1 Bohr = 52.9 pm
Example: In Bohr's model for a hydrogen atom, what is the radius of the three smallest orbits?
Answer:
For the smallest orbit, n=1, radius = (52.9 pm)(12) = 52.9 pm, or 1 Bohr
For the second smallest orbit, n=2, radius = (52.9 pm)(22) = (52.9 pm)(4) = 211.6 pm, or 4 Bohr
For the third smallest orbit, n=3, radius = (52.9 pm)(32) = (52.9 pm)(9) = 476.1 pm; or 9 Bohr
Example: what is the radius of the third orbit of hydrogen in Bohrs?Answer: r = a(3)2 = 9a, or 9 Bohr.
Exercise: For Bohr's model, if "a" is the radius of the first allowed orbit of hydrogen, what is the radius of the third allowed orbit? A. 3a, B. 6a, C. 8a, D. 9a
Answer:
Energy Quantization
Bohr also derived the energy of an electron in the nth orbit to be
E = -R / n2
where R is called the Rydberg constant, which is equal to 13.6 eV or 2.18x10-18 J. Because n is restricted to positive integer values (n=1, 2, 3, etc.), not every value is allowed for the energy. We say that the energy of the electron is quantized. Thus, Bohr's theory is known as the old quantum theory. In modern quantum theory, the notion of electrons traveling in well-defined orbits around the nucleus is no longer acceptable. However, energy quantization is still accepted.
Example: In Bohr's model for H, what is the energy of an electron in the 2nd orbit?
Answer: In the second orbit, n=2. Therefore:
E = -13.6 eV / (22) = -3.4 eV
or
E = -2.18x10-18 J / (22) = -5.45x10-19 J
Note: The SI unit for energy is J, but eV (electron volt) is commonly used for energies of electrons. One electron-volt is the energy gained by an electron accelerated through a potential of 1 volt and is equal to 1.60x10-19 J.
Ionization Energy
The value of E is negative because the potential energy is (arbitrarily) defined as zero when the electron is at infinite distance from the nucleus. What this means is that you need to provide the electron with energy to be able to escape the atom; the minimum amount of energy needed is called the ionization energy.
Example: Using the Bohr model, calculate the minimum energy needed to remove an electron from the first orbit.
Answer: The electron is farthest from the nucleus with n=∞ (infinity), where E=0. In the first orbit, E=-13.6 eV. Therefore, the energy needed, called the ionization energy, is
Ionization Energy = E∞ - E1 = 0 - (-13.6 eV) = 13.6 eV
If more than this is provided, the excess energy becomes kinetic energy of the electron.
Exercise: For Bohr's model, the energy of an electron in any of the orbits is a negative value. This means that...
A. the electron is moving in a clockwise direction
B. the electron is moving counterclockwise
C. the electron has imaginary speed
D. none of these
Answer:
Spectral lines
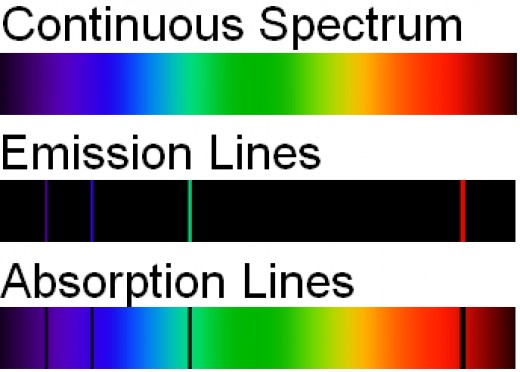
Explaining line spectra of atoms
When atoms absorb or emit light, only certain colors are observed. See above Photo which shows the light emitted or absorbed by hydrogen atoms in the visible region of the electromagnetic spectrum. The top part of the figure, the continuous spectrum, shows the full range of wavelengths in the visible region (which our eyes perceive as colors). The middle and bottom part of the figure are examples of what are known as line spectra. Not every color is observed; the ones that are observed appear as very sharp lines. For more about atomic line spectra, visit these websites:
To explain the line spectrum of hydrogen, Bohr assumed that
1. energy from light is available only in discrete bundles (called "quanta"); this is the same bold assumption that Max Planck and Albert Einstein made earlier to explain blackbody radiation and the photoelectric effect. Each bundle of energy is called a photon and the photon energy is proportional to the frequency.
Ephoton = h ν
where h is Planck's constant (6.626x10-34 J s) and ν is the frequency of the light. In terms of wavelength (λ),
Ephoton = hc / λ
where c is the speed of light (2.998x108 m/s).
2. light is absorbed when a photon collides with an electron, but the energy of the photon must be just the right amount to promote the electron to a higher allowed orbit
Ephoton = E(higher orbit) - E(lower orbit)
3. an electron in a high orbit (n>1) can lose energy by emitting one photon of light. The electron must end up in an allowed lower orbit, so the photon energy must be equal to the difference in the energies of the higher and lower orbit.
Ephoton = E(higher orbit) - E(lower orbit)
You may find it useful to visit these websites:
Example: Using Bohr's model, calculate the frequency and wavelength of photon produced when an electron jumps from the third orbit to the second orbit of hydrogen.
Answer: First, calculate the energy of the photon.
Ephoton = E3 - E2
= -R/32 - (-R/22)
= - 1.89 eV = 3.02x10-19 J
Then, calculate the frequency (ν) given that Ephoton = hν.
ν = (Ephoton ) / h
= (3.02x10-19 J) / (6.626x10-34 J s)
= 4.56 x 1014 s-1
The wavelength (λ) can be calculated from the frequency since ν = c/λ.
or it can be calculate the photon energy since Ephoton = hc/λ
λ = hc / Ephoton
= (6.626x10-34 J s) (2.998x108 m/s) / 3.02x10-19 J
= 6.58x10-7 m, or 658 x 10-9 m, or 658 nm
This is the red line in the emission spectrum of hydrogen.
Exercise: According to Bohr's model, what is the energy of the photon released when an electron jumps from the third orbit to the second orbit of the hydrogen atom?
A. 13.6 eV, B. 1.89 eV, C. 10.2 eV, D. 2.27 eV
Answer:
Exercise: According to Bohr's model, which of the following wavelengths will not be absorbed by an electron in the first orbit?
A. 142 nm, B. 122 nm, C. 97.5 nm, D. 94.0 nm
Answer:
Hydrogenic Ions
The Bohr model also explains line spectra of ions with only one electron. These are called hydrogenic or hydrogen-like ions. For example, it works for He+ and Li2+. A He atom has two electrons; a He+ ion has only one electron. Similarly, a Li atom has 3 electrons, Li+ has two, and Li2+ has only one. In these cases, the radius of the nth orbit is
r = (52.9 pm) n2/Z,
and the energy of the electron is
E = -R Z2/n2
where Z is the atomic number (the number of protons in the nucleus).
Example: what is the radius and energy associated with the 2nd allowed orbit of Li2+.
Answer: Referring to a periodic table, we find that the atomic number of Li is 3. There are 3 protons in the nucleus of a Li atom. There are also 3 protons in the nucleus of Li2+. Therefore:
r = (52.9 pm) (2)2 / 3 = 70.5 pm
E = -(13.6 eV) (3)2 / (2)2 = -30.6 eV
Failures of the Bohr Model
It fails to explain why some spectral lines are brighter than others.
It is not able to explain line spectra of any atom or ion with more than one electron.
The notion of well-defined orbits for electrons is inconsistent with Heisenberg's uncertainty principle. One consequence of the principle is that it is impossible to precisely and simultaneously determine the location and velocity of an electron, which is exactly the kind of information that an orbit provides. For a good video explaining Heisenberg's principle, watch here. While this video talks about a beam of light, the same behavior is observed for a beam of electrons. The behavior of the beam going through the slit is called diffraction, a characteristic of waves. The uncertainty is due to electrons behaving like a wave. For another video showing wavelike behavior of electrons, double-slit diffraction, watch here . For more on diffraction, visit the following websites:
Exercise: Which of the following is true regarding the Bohr model?
A. it assumes that electrons move around the nucleus in elliptical orbits
B. it only works for atoms or ions with only one electron
C. it assumes that electrons will eventually crash into the nucleus
D. it predicts that light is produced when an electron transfers from a smaller orbit to a larger orbit.
Answer:
Spectral Lines: Modern Interpretation
In modern quantum theory, orbits for electrons are no longer accepted, but light emission and absorption are still explained by assuming that energy of photons absorbed or emitted must match gaps between quantized energy levels of particles (atoms, molecules, or ions). Light absorption occurs when the photon energy is equal to the energy gap between two allowed energy levels. When light is emitted, the energy of the photon produced is also equal to the energy gap between two allowed energy levels.
E photon = E(upper allowed level) - E(lower allowed level)
Example: An atom loses 6.5 eV of energy by emitting light. What is the energy of the photon released?
Answer: The photon energy is equal to the energy lost by the atom, 6.5 eV
Example: A molecule absorbs light with a wavelength of 250.0 nm. How much energy did the molecule gain?
Answer: The energy gained by the molecule is equal to the energy of the photon.
Ephoton = hc/λ
= (6.626x10-34 J s) (2.998x108 m/s) / (250.0x10-9 m)
= 7.95x10-19 J, or 4.97 eV.
References
© 2015 Discover the World