Buoyancy and Archimedes's principle

On April 15, 1912, at 11.40 on ship's time Titanic's lookout spotted an iceberg ahead of the ship. Slightly less then 3 hours later Titanic sunk. As we know, five of its watertight compartments were broken and there were no hope for the ship. Thus, quite small iceberg had sunk the biggest ship in the world. However, it worth to note that only a part of the iceberg was visible while its major part was under water. More precisely, only about 11% of an iceberg is above water.
What an iceberg and a plane have in common? The same force keeps the two bodies floating. The buoyancy is the force that diminish gravity, keeping an iceberg on a surface of water and a plane in the air. This phenomenon is firstly discovered by Archimedes of Syracuse and described in his book On Floating Bodies. The Archimedes principle states that a body immersed in a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
Firsty, the Archimedes's principle will be explained in detail. Than the other related phenomena including surface tension andcapillary action will be outlined.
Archimedes of Syracuse - Eureka!
Reportedly, Archimedes was asked by a king to check whether his crown is build by the pure gold or might some cheaper metal like silver is put into the crown. The anecdote says that one day Archimedes had a bath in a public bath in Athens, when the idea of solution came. Archimedes promptly came out of the bathtub starting to run crying “Eureka!” (In Greek, which means “I found is!”). In his excitement, he forgot to dress.
What was so ingenious idea? Obviously, the volume of submerged body is the same as the volume of displaced liquid. We can say that liquids are incompressible, especially for practical purposes. Furthermore, the crucial Archimedes's idea was that a submerged body loses weight that is equal to the weight of displaced liquid. This means that the crown and the gold of the same mass can be placed on the scale. Then the entire system is immersed in water. If the system remains in balance under water, then the crown is build of pure gold. Otherwise, part of gold is replaced by some cheaper metal. The anecdote says that the experiment has proved that silver had indeed been mixed into the crown. However, nowhere in his writings Archimedes mentioned this story.

Archimedes's principle
As we know, our kick under water is of much less strength than usually. We lose our weight under water. If we would have an opportunity to weight in the water we will find much less weight than we normally have. Imagine to take a dynamometer in order to measure the weight of some body in two cases: normally and immersed in water. The difference is significant.
In his book on hydrostatics, titled On Floating Bodies, Archimedes stated: “Any object, wholly or partially immersed into a fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.” This phenomenon is known as Archimedes's principle.
The force that acts on the body up is called buoyant force or buoyancy. But what is the cause of this force, that is characteristic for fluids? Buoyancy appears as a consequence of the hydrostatics pressure. Namely, there is the difference in pressures between the upper and lower side of an immersed body. If the next section the full quantitative explanation will be done.
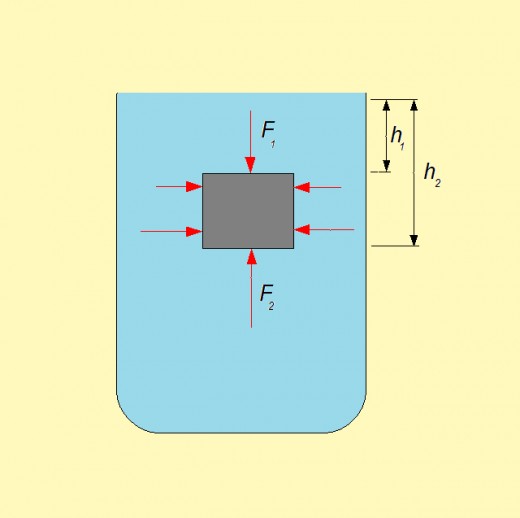
Buoyant force
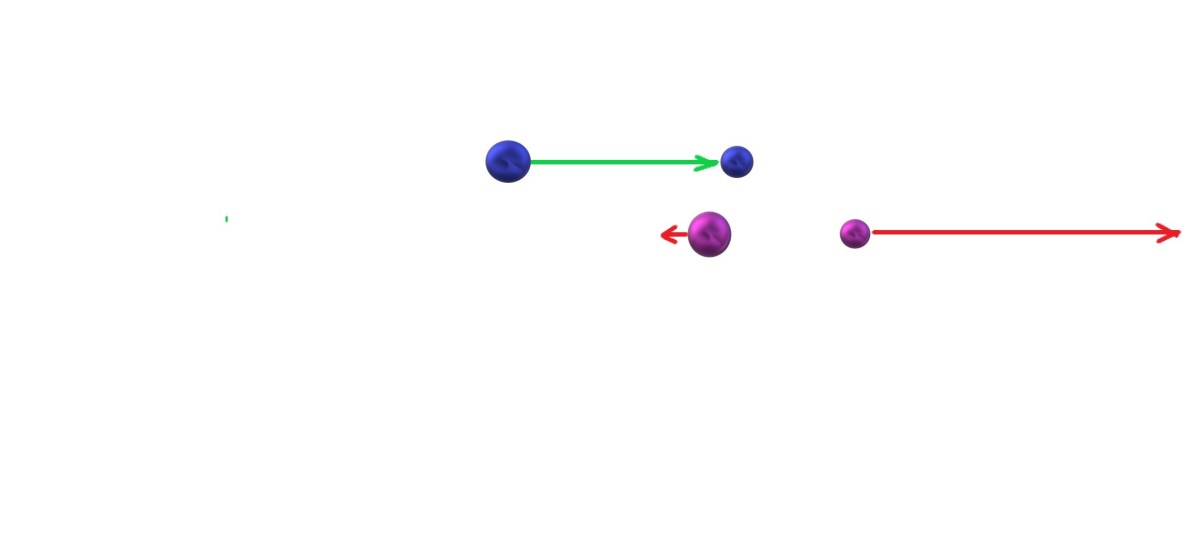
Imagine a body submerged in water, as the figure presents. Because of hydrostatic pressure, forces act on all sides of the body. According to the basic characteristic of hydrostatic pressure, pressures on the same depth are equal. This means that forces towards left side, and towards right side of the body at the same depth will annul each other. On the other hand the total force on the upper side and the total force on the lower side will differentiate.
The difference of these forces (F1 and F2) is the buoyant force Fu., Fu = F2 – F1 . Having known that the pressure is the ratio of the force and the area where that force acts, we have
Fu = F2 – F1 = p2 *A – p1 *A.
It is known that in the liquid of the density φon the depth h the hydrostatic pressure P is P = φ * g * h. Now we substitute the equation for hydrostatic pressure.
Fu = p2 *A – p1 *A = φ * g * h2 * A- φ * g * h2 * A
Fu =φ * g *Δ h * A
Product of the area and the difference in depth is the volume of body:
Fu =φ * g *Δ h * A = φ * g *V
Thus, the buoyant force is a product of the density of liquid, the volume of the body and the gravitational acceleration,
Fu = φ * g *V.
There are three possible cases of the relation between buoyant force and weight force of an immersed body. If the buoyancy equals the weight, the body floating in the water. If the weight is greater, the body will fall down. It will be uniformly accelerated motion, but with a smaller acceleration than of free fall. If however the buoyancy exceeds the weight, the body will accelerates up. Having in mind that on every body immersed into water acts a buoyant force equal in magnitude to the weight of displaced liquid, the crucial condition whether a body will sink or float is the density. If the immersed body is more dense that water, it will sink. Otherwise, if the body is less dense than water, it will float.An remarkable example is an iceberg, which floats on water. Around 11% of an iceberg is visible i.e. above water while the rest of ice is underneath the surface.


Do it yourself – physical experiment in your home!
-
Pour water into some glass.
-
Prepare a paper clip and a coin.
-
Carefully lay a paper clip on a water surface. Do the same with a coin.
Although both of items regularly immerse into water, it can stay at a surface thankfully unbalanced cohesive forces on surface molecule layer.
Surface tension
Water striders are able to stay at top of liquid. If we are careful enough, we can achieve a paper clip to stay at top of liquid. It is even possible to place a coin at the top of water. How come that metals like a coin, which surely submerge into water, is possible to stay at top of liquid? This phenomenon is known as surface tension and it appears because of cohesive forces between molecules of liquid.
Each molecule in the liquid interact with neighboring molecules. The net force of these interactions is zero, since the molecule doesn't move. However, the net force of molecules in the surface layer of liquid is not zero. That molecules are not surrounded by the same number of molecules in every direction since they are on the border between the two fluids. This explains that in case of water and air, additional weight can be put on surface molecules.
Of course, this means that regularly there is a certain internal pressure in a liquid. It appears because forces on surface molecules are unbalanced. In addition to putting things on a liquid surface, an interesting manifestation of surface tension is the shape of liquid droplets.
As experience teach us, water droplets form a spherical shape. Clearly, this is the consequence of cohesive forces of the surface molecule layer.
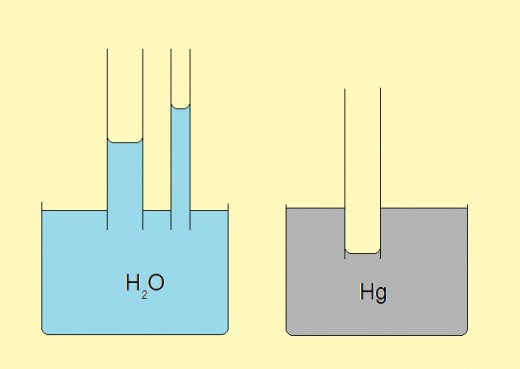
Capillary action
Cohesive forces act among identical molecules whereas between molecules of two different substance there are adhesion forces. This fact has a special manifestation on the border between two substance, say liquid and glass. Depending on the relation between the cohesive and adhesive forces, liquid on the border will be curved, either upwards of downwards. This phenomenon is known as capillarity action. A special effect is obtained when a tiny tube is partially immersed in a liquid. In this case the law of connecting vessels doesn't work but the level is either higher or lower than the level of the rest of liquid.
Typical examples are those with water and mercury. Water in a glass is twisted upwards along the border with glass. Consequently, the level in a tiny tube immersed into the glass will rise (depending on the tube width). The opposite case is with mercury.
Let a contact angle – an angle between the tube and liquid denote by α, the radius of tube by r, the density of liquid by ρ, gravitational acceleration by g and the liquid-air surface tension by γ. Then, for the height h it holds
h = 2 * γ * cos α / ρ * g * r.
For the most common situation, water – glass, the equation above gives h = 1.48 * 10-5 / r. For example, in 0.4 mm diameter glass tube the level of water will rise 70 mm.
At the end, let explain quantitatively why around 11% of an iceberg is hidden. Thus, since the iceberg is stable, the net force on it is zero. This means that the buoyant force equals gravity, Fu = Fg. The buoyant force acts on immersed part of ice, V /x . It holds ρ * g * (V / x) = m * g which gives ρ * (V / x) = m. Now we substitute the mass of the iceberg,ρw * (V / x)= ρi * V. Finally, x = ρw /ρi = 1030 / 920 = 1.11.
Case studies
A piece of glass weights 1.4 N in the air and 0.8 N in water. What is the density of this glass?
Solution: Weight of the glass in water Fg(H2O) equals the vector sum of buoyant force Fband weights of glass Fg, Fg(H2O) = - Fb + Fg. It follows
Fg(H2O) = ρ(H2O) * V * g + Fg,
which gives the value of glass volume
V = 0.56 N / (1000*10 kgm-3)
Once knowing the value of volume and having m * g = 1.4 N, we use defining equation for density to reach a final result.
ρ = m / V = … = 2500 kgm-3
A short quiz - check your knowledge!
view quiz statisticsThe lower half of a vessel is filled by mercury and the upper part by water. A ball floats in the liquid so that half of its volume is in mercury and the other half in water. What is the density of the ball?
Solution: The weight of the ball is balanced by the two buoyant forces. Each of the buoyant forces act on the half of ball.
Fg = ½ * ρ1 * g * V + ½ * ρ2 *g * V
m = ( ½ * ρ1+ ½ * ρ2 ) * V
m/V = ( ρ1+ ρ2 ) / 2
ρ = ( ρ1 + ρ2 ) / 2
So, the density of ball is half of the sum of the two density. The density of water is 1000 kg/m3 and for mercury the density is 13600 kg /m3.