Centripetal Force


A Fun Yet Dizzy Time
One of my childrens favorite things to do is for me to hold their hands and rotate them around until they are horizontal to the floor. We spin and spin and then fall over, dizzy and full of laughs.
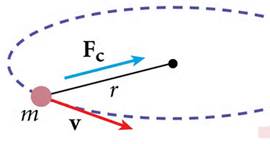
Most of us do not think about the forces that are working during such casual type play. One of the forces that cannot be ignored in this instance is Centripetal Force. Centripetal force is the inward force exerted on an object during uniform circular motion.
Centrifugal force is the force exerted away from an object in circular motion and will have to be discussed in another hub.
Centripetal force is the force that keeps the Earth in orbit around the sun and keeps atomic electrons moving around the nucleus.
I wrote a hub titled uniformly accelerated motion earlier where we discussed free fall. In this hub we will discuss what happens when an object is in uniform circular motion. We will also investigate different types of centripetal force apparatus and how they can be used to visualize the concept of uniform circular motion in a laboratory setting.
What is Centripetal Force?
For an object to stay in uniform circular motion it requires a center seeking force to hold it in orbit. This force is called a centripetal force. In the case of a person swinging a ball on a rope over their head the person is supplying the force that moves to the ball through the rope.
If the rope breaks or the person releases the rope the ball would no longer hold its orbit and would fly out in the direction of its tangential velocity.
The equation for centripetal force is:
F(c)=ma(c)
Where:
F(c) = Centripetal Force
m = Mass
a(c) = Centripetal Acceleration
Things get a little confusing here but hold on and I will explain the best I can. An object moving in uniform circular motion moves with a constant speed but not a constant velocity.
The velocity changes because the direction of motion is constantly changing.
Centripetal acceleration, a(c), is tangential or orbital speed of the obect, v, divided by the radius of the circle, r.
a(c) = v^2/r
Newton's Second Law states that F=ma, or a force equals its mass times its acceleration. With this in mind we can deduce:
F(c) = ma(c) = mv^2/r
Or centripetal force equals the mass of the object times its orbital speed squared divided by the radius of the circle.
The orbital speed can be determined:
v = 2(pi)r/T
Where T is the amount of time it takes to go around the circle once. The above equations only work in the case of uniform circular motion.



How Can You Measure Centripetal Force?
There are three different apparatus used to measure centripetal force of an object in uniform circular motion.
The first would be:
Manual Centripetal Force Apparatus
A hand-held apparatus that works by rolling a rotor between the thumb and forefinger. This action sends a mass bob into circular motion.
A pulley mounted at the base is then used to take the necessary measurements by recording the spring tension supplied for the uniform circular motion to occur.
Centripetal Force Apparatus with Variable Speed Rotor
When a mass located on a spring is set into circular motion by a motor a pointer (P) will line up with an index screw (I) when uniform circular motion is achieved. The distance between the obect and the index screw when the pointer is lined up is the radius.
The final apparatus is similar to the Centripetal Force Apparatus with Variable Speed Rotor with a digital monitor included.
Closing Thoughts
Now when I spin my children around I am reminded of the forces that are acting upon me and my child.
A good time is still had by all, but this time a little understanding of how the physical world works has added a sense of wonder to the joy.