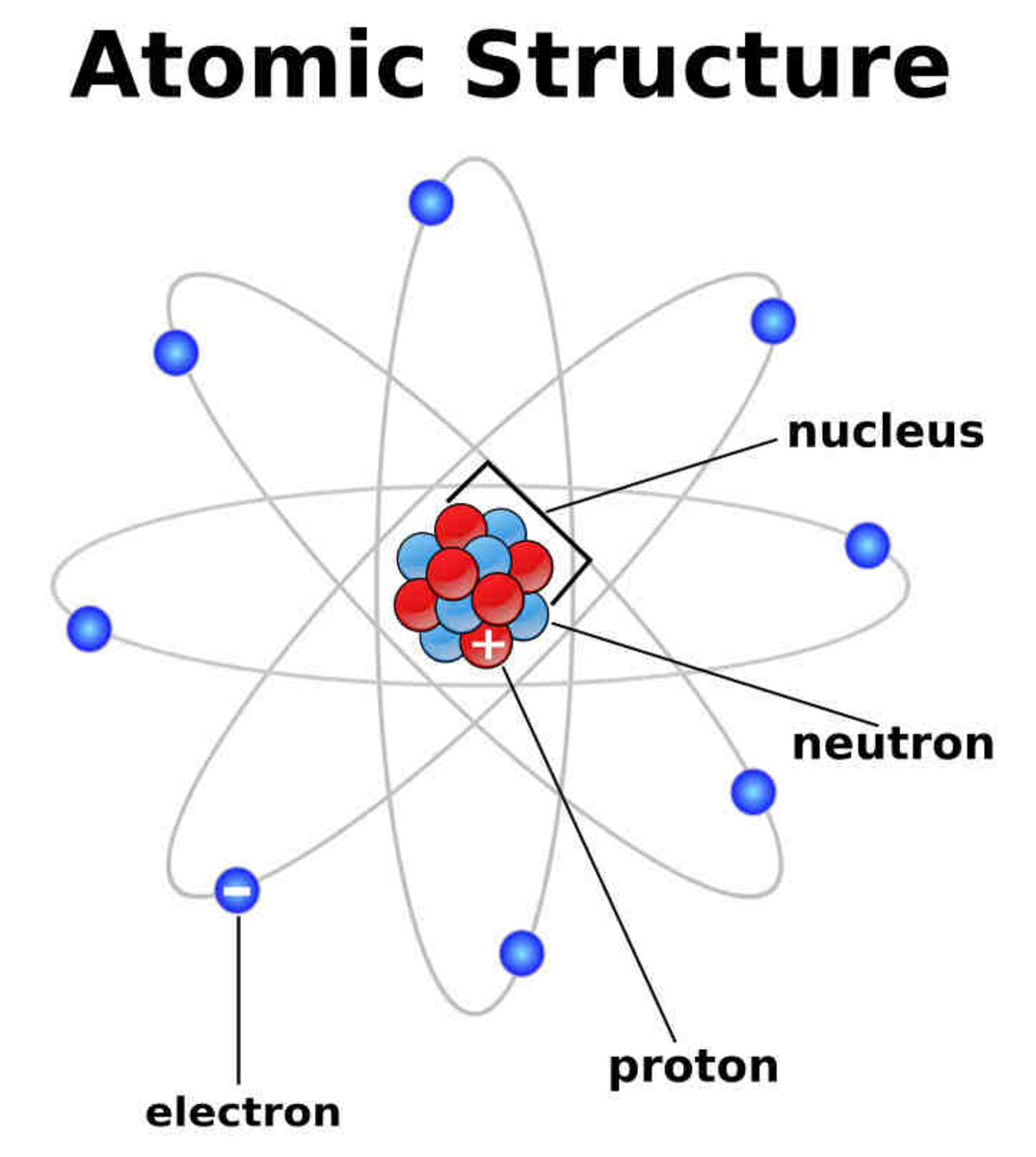
Chemistry Concepts Explained

I'll be periodically posting basic explanations for various chemistry topics. The information will come mostly from Modern Chemistry by Raymond Davis and a few others (published by Holt, Reinhart and Winston).

I'm working on putting together step-by-step instructions for my students, so I figured I might as well use them here as well.

If there is a specific topic you would like covered, you can certainly ask in comments or in PM. I can't make any promises, but I will try to explain as thoroughly as possible. If you have suggestions for things I should cover, I'm all ears.

NEW STUFF FIRST

1. Look at a Periodic Table of the elements and find which group the element in question is located. Most of the ones you'll be given will be from the main groups (1,2, 13, 14, 15, 16, 17, 18).
2. Determine how many valence electrons the element should have. The # of valence electrons = the last digit of the main group #. ie. Li is in group 1 it has 1 valence electron. S is in group 16, it has 6 valence electrons.
3. Draw the symbol for the element and draw one dot to represent the valence electron. There are some conventions about what order to add the dots in. I'm personally not that picky. I tell my students my only stipulation is that they put a maximum of 2 electrons on any given side of the element's symbol. This helps them with the counting. Example of lithium. Example of sulfur.

I'll use H2O as an example.

1. Count the valence electrons you need to account for with the structure. H is in group 1, so they will both have 1 valence electron. O is located in group 16, so it will have 6 valence electrons. (The Math: 1 + 1 + 6 = 8 e-)

2. Put the central atom down and connect each other atom with one bond. Generally, the least electronegative element is written first and is the central atom. However, H may NEVER be the central atom. (Reasoning: H only has 1 valence e-, so it only forms 1 bond. A central atom must be capable of bonding with more than one atom.) O is the central atom. Bond it once to each hydrogen.

3. Add lone pairs of electrons to every atom that needs a complete octet. The vast majority of elements will want a complete octet of electrons because that offers the most stability. 2 lone pairs of electrons will be added to O. Note: Most elements like to have 8, but H, Be, B are exceptions, fall short of the octet.

4. Check to see that your structure has used the correct number of electrons. 2 shared pairs, 2 lone pairs = 8 electrons. Link to a blog that has basically the same instructions + a picture.

Another example that requires double bonds. CO2

1. valence e- = 4 + 6 + 6 = 16

2. C is the central atom, so write it down and then add an O to either side with a single bond connecting them.
O - C - O

3. Add lone pairs of electrons so that everything has a stable octet. 3 lone pairs for each O and 2 lone pairs on the C.

4. Count the electrons you used. 8 from each oxygen, including the shared bond with C + 4 from the lone pairs on C = 20 e. This is too many. To cut down on the number of electrons used in the structure, add another shared pair of electrons between the C and O. We want to come down by 4 electrons, so 2 double bonds.

O = C = O

Fix the octets. Each O needs two lone pairs of electrons, but the C needs none b/c it has 4 shared pairs of electrons (8). Recount the electrons used. 8 from each O, including the electrons locked in bonds with C. 8 + 8 = 16e-. Picture of CO2.

I will use sulfite (SO3^-2) as an example.

1. Count the valence electrons as usual. The electrons that must be accounted for in the structure are slightly different this time though because you will need to add or subtract accordingly as dictated by the charge. People get tripped up here because a charge of +2 means that 2 electrons have been lost and a charge of -2 means 2 electrons have been added. Sulfate's electron math: (6 from S) + (3 x 6 from O) + (2 from charge) = 26 e-

2. Write the central atom and bond each other atom to it once. S is central and it will be bonded once to each O.

3. Fill the octets. Each O needs 3 lone pairs of electrons. S needs one lone pair since it is only bonded 3 times, once to each O.

4. Count the electrons used. 8 electrons around each O, including the shared bonds with S. (8x3 = 24 e-). 2 electrons from the shared pair on S. Total = 26 e-. Note: this structure is correct but does not consider the topics of resonance or formal charge. (My main concern is that the correct # of electrons be used and the octets be filled. In layman's terms, resonance means that there is more than one legitimate structure and the "real" structure is actually a hybrid of those.) Here's a link to a Youtube video that goes way deeper.

Molarity = moles solute / Volume of Solution in Liters

Molarity is a common unit for concentration. In words, the formula means you take the moles of the solute and divide by liters of the whole solution.

Complications:There are several things a teacher can do to make the problem more complicated, such as giving you the volume in a different unit like mL or the amount of solute in a different unit like grams.

If you're given the volume in mL, simply convert to L by dividing by 1000.

If you're given the amount of solute in grams, use the unit factor method (conversion factors) to convert from grams of the substance to moles. You will need to know the molar mass to do this. (Molar mass is the amount of grams per one mole of the substance).

Sample Question: What is the Molarity of a solution if 2 L of solution contain 6 moles of NaCl?

M = (6 moles)/(2 L) = 3 mol/L or M (note: the unit for Molarity can be a capital M or mol/L)

More Complicated Sample Question: What is the Molarity of a solution if 345 g of NaCl is dissolved in enough water to make 125 mL of solution?

Calculating the molar mass of NaCl is simple since the formula only contains 1 Na and 1 Cl. Add ~23 g (Na) + ~35.5 g (Cl) = 58.5 g/mol NaCl

345 g NaCl x (1 mol NaCl/ 58.5 g NaCl) = 5.90 mol NaCl

125 mL x (1 L/ 1000 mL) = .125 L

M = (5.90 mol NaCl)/ .125 L = 47.2 M

Other versions of the Molarity formula:

Solve for moles: mol = M x L

Solve for liters: L = mol / M (algebraically, this one seems to be the toughest for students to obtain)

Note: For Honors and Chemistry, your quiz/test will clearly mark which type of compound you are naming.

Step 1: Master the prefixes—mono=1, di=2, tri=3, tetra=4, penta=5, hexa=6, hepta=7, octa=8, nona=9, deca=10

Step 2: Observe the formula you are trying to name. For example, let’s try to name N₂O.

a) Consider the prefix immediately to the right of the first element symbol. It is 2. Write the appropriate prefix and the element name (all as one word). So far we have: dinitrogen. Please note that if there is no number immediately to the right of the first element, we do NOT write down the prefix mono. Instead, simply report the element name.

Note: be careful when spelling phosphorus (it is NOT “ous” at the end)

b) Consider the prefix immediate to the right of the second element symbol. There is none. In such cases automatically use the prefix mono, which means there is only one of that element. This part is tricky when you first come upon it, so read carefully. Write down the appropriate prefix, the main part (usually first syllable) of the element name, and the suffix/ending –ide (all as one word, separate from the first.) Now, if we add it to what we already had, we get: dinitrogen monooxide.

Note: be careful when spelling fluoride (“u” before “o”)

Step 3: Adjust for special cases. If there are any cases where two “a’s” or two “o’s” or “a” and “o” would be right next to each other, drop the “a” or “o” from the prefix. In this case, the name must be adjusted to: dinitrogen monoxide. Two “i’s” next to each other are fine; ie. triiodide

Step 4: Practice (both ways name à formula; formula à name). There are many websites out there for naming binary molecular compounds. Some are more useful than others.

Some examples to practice with:

SF₆ = sulfur hexafluoride CCl₄ = carbon tetrachloride

CO = carbon monoxide P₄S₁₀ = tetraphosphorus decasulfide

N₄O₂ = tetranitrogen dioxide NF₃ = nitrogen trifluoride

Step 1: Memorize a list of common cations and anions (positive and negative ions respectively). If you’re doing a homework assignment and have not yet mastered such a list, simply refer to one. (If you’re in one of my classes, this is not an optional step. I will generally not let you use an ion chart on the quiz or test. Never say never, yet for now accept that “no” is the answer to that question.)

Step 2: Write down the formulas for the positive and negative ions. (This is not a true requirement but very useful when learning how to write ionic chemical formulas. Take it as a good habit.) Let’s practice with gold (III) nitrate. Gold (III) is Au⁺³ and nitrate is NO₃^-1.

Note: It is not absolutely necessary to write the charge on nitrate as -1. Having 1- or just the “-” sign is good enough. However, students commonly mistake nitrate as NO with a negative 3 charge when they write only the “-” sign.

Step 3: Consider the charges. Remember that the ultimate goal of writing an ionic chemical formula is to make the charges equal and opposite. Au⁺³ has a +3 charge and NO₃^-1 has a -1 charge. Determine how many of each type of ion you would need to make their charges balance. In this case, I would need 1 of the Au⁺³ and 3 of the NO₃^-1. Often, this will mean simply “switching” the absolute value of the charges. However, if you do this, remember to reduce wherever possible. (So, if my charges had been +4 and -2, switching would tell me 2 of the +4 and 4 of the -2, which would give me +8 and -8 … equal and opposite, yes, but not the simplest version of this. 2 and 4 can both be reduced, so your answer should involve only 1 of the +4 and 2 of the -2, giving you +4 and -4 charges. Yes, I do realize I just switched p.o.v.’s in my writing… this is precisely why I don’t teach English.) 

If you’re having trouble with this step, consider it in terms of money. If you want something that is $.75 (like a single stick of gum) but you only have quarters, you will need 3 of them because each quarter is worth $.25.

Step 4: Use the numbers you figured out in step 3 as subscripts (the # of each ion you would need to make the charges equal and opposite). Write down the ion symbol in its entirety but without the charge and put the subscript down immediately to the right of this ion symbol. If you only need 1 of something do NOT use a subscript. The ion symbol itself will suffice. So far we have: AuNO₃₃. Something’s wrong though, we don’t want 33 O’s. We want three of the nitrate ions. We will need to add parentheses to ensure that our meaning is clear: Au(NO₃)₃. If you don’t want to be constantly fixing that mistake, just remember that if you need more than 1 polyatomic ion—that is a group of covalently bonded atoms with an overall charge—you will need parentheses to encase the ion and set it apart before putting your subscript in. (Run-on sentence, horrors!)

Step 5: Check your answer. If gold (III) is worth +3 and I have 3 nitrates, each worth -1, my charges should be equal and opposite. 1 and 3 do not reduce further, so this is the correct answer.

Step 1: Accept that you’re going to have to essentially work backwards. Let’s work with the example Fe₃(PO₄)₂ because it’s nice and difficult. Write down the cation and anion (positive and negative ion) names. Iron phosphate. Leave a little extra space in between iron and phosphate just in case you need to put in a roman numeral. (Note: this is the stock system.)

Step 2: Consider whether or not the positive ion is one that can have more than one form. If it is not, then you are done. Adjust for spacing if you left excessive amount of space between the words. If it is, then think of the possible forms that positive ion could have. Iron can be Fe⁺² or Fe⁺³.

Step 3: Determine which positive ion you have in your formula. The charge on the negative ion does not change; phosphate will always be PO₄^-3, therefore, it will always have a -3 charge. Look at the subscript next to the negative ion and multiply that subscript by the charge of the negative ion to get the total negative charge in this formula. There is a subscript of 2 next to the phosphate, so the total negative charge will be -6.

Step 4: All ionic chemical formulas should be neutral, meaning total positive charge is equal in magnitude to the total negative charge. If the negative charge is -6 then the positive charge must be +6. Take this total positive charge and divide by the subscript to get the charge on just one of the positive ions. +6 divided by the subscript of 3 will be +2; therefore, this iron ion must be iron (II).

Step 5: Write down and then check the compound name: iron (II) phosphate. Iron (II) is a +2 ion and phosphate is a -3 ion, so if you wanted to rewrite the formula you would need 3 of the iron (II)’s and 2 of the phosphates. This should give you your original question back.

1. Switching the cation and anion (positive and negative ions). Positive ions or names always come first in ionic chemical formulas.

2. Writing CO instead of Co. You may say, what’s the big deal, but inside, I flinch because I have to mark it wrong. Capital “C” next to capital “O” (yes, I know that’s redundant) means 1 carbon and 1 oxygen. On the other hand, Co is the symbol for the element cobalt.

3. Rampant parentheses. If you don’t need them to set apart a polyatomic ion, you can’t have them.

4. Missing parentheses. If you need them, you MUST have them.

5. Not reducing when you need to. If you have lead (IV) oxide the formula is PbO₂ NOT Pb₂O₄.

6. Needlessly reducing. Poor sulfate has had its number of oxygen slashed more times than I can count. Leave sulfate alone (young chemistry bullies)! Gold (I) sulfate is written Au₂SO₄ NOT AuSO₂.

7. Not putting in subscripts. Subscripts are your friends; use them to bring balance to the poor fledgling formulas-to-be.

8. Mistaking the subscript in a polyatomic ion for the subscript denoting the number of ions. (Refer to 6. Sulfate ceases to be sulfate if you change the number of oxygen in its formula, SO₄^2-.)

These calculations are basically the same just with different units. I stress the importance of the conversion factor method at first to get the format down, and then, once we get to % composition, I just let the students use the shorthand version of molar mass.

Step 1: You must have the correct chemical formula
Step 2: You will need a periodic table to look up the molar mass or the amount of amu per atom
Step 3: You'll probably need a calculator to do the multiplications and addition.

1. Calculate the formula mass of iron (III) oxide

Chemical Formula: Fe₂O₃

2 atoms Fe x (55.847 amu/ 1 atom Fe) = 111.694 amu

3 atoms O x (15.999 amu/ 1 atom O) =     47.997 amu _

                                                                   159.691 amu -->159.69 amu

2. Calculate the molar mass of mercury (II) carbonate

Chemical Formula: HgCO₃

1 mol Hg x (200.59 g Hg/ 1 mol Hg) = 200.59 g Hg

1 mol C x (12.011 g C/ 1 mol C) =       12.011 g C

3 mol O x (15.999 g O/ 1 mol O) =      47.997 g  O _

                                                       260.598 g/mol -->260.60 g/mol HgCO₃

You'll have to rely mostly on what your specific teacher wants, but in general, significant figures are based on what can be definitely measured plus one digit. So, for example, if you have a metric ruler you could see if something is 2.24 centimeters. That last digit is estimated though because there is no definite line for you to measure and see for sure. So, one person may look at the metric ruler and say something is 2.27 cm and another say 2.26 cm. I would say, in most cases, it doesn't matter which you choose, so long as the rest of your calculations follow consistently.

Scientific notation follows the pattern M x 10^x (your M value must be b/t 1 and 9).

A few examples of numbers and the # of sig figs they contain:
2 232 000 000 is only 4 sig figs
43 432 000 003 is 11 sig figs
3443.00 contains 6 sig figs (By specifically putting in the 0's after the decimal point, I am deeming them significant. The assumption is that whatever instrument this number was derived from could be estimated to that second 0.)

Note: If I wanted to indicate the first number 2232000000 to 5 sig figs, I would simply draw a line over the top of that first 0 (the fifth digit from the left)

When doing problems, you want to show your final answer to the least number of sig figs.

Mathematical operations:

Addition and subtraction - line up the decimal points. If I wanted to add 22.46 + .2569, I would need to line up the decimal points, do the addition, and then round to two decimal places, since we are assuming that the 6 in the first number is already an estimated digit.
22.46
+ .2569
22.7169 --> 22.72

Multiplication in scientific notation:
Multiply the M values and add the exponents. Then, adjust for significant figures and your new M value. For example, if your problem is (2.5 x 10^2) (5.0 x 10^4), you would take 2.5*4 to get your new M and then add 2+4 to get the new exponent.
2.5 x 10^2
x 5.0 x 10^4
12.5 x 10^6 --> 1.25 x 10^7
The only part that can get really tricky is if you have a negative exponent, then you may be adding a negative number (in essence subtracting).

Division in scientific notation:
Divide the M values and subtract the exponents. Then, adjust for sig figs and your new M value.

The easiest way to do stoichiometry problems is to get good at the conversion factor method. It follows some basic steps:

1 – start by writing down the number and unit you would like to convert

2 – write a multiplication sign and the conversion factor you wish to use. What you

go from should go on the bottom and what you go to should go on the top.

3 – repeat step 2 as necessary; many conversions take several steps.

That might sound confusing but let do an example with money. Let's just say the current Euros to dollars conversion rate is 1 Euro = 1.43 dollars. If I want to buy something that costs 8.00 Euros, I could set up a conversion factor to get from euros into dollars, so I would know how many dollars to pay.

8.00 Euros x (1.43 dollars/ 1 Euro) = 11.44 dollars

The unit I wanted to change from (Euro) was put on the bottom so it would cancel with my original unit. The unit I am left with (dollars) is on top, and after cancellation, it is the only thing left.

The conversion factor method is useful in Chemistry because you can perform calculations involving atoms/ molecules, moles, and mass.

Take the analogy of a typical address. A person lives in a specific country, state, county/municipality, city/town, street, and house/apartment. Beyond that, people have names to distinguish those who live at the same address. They same sort of holds true for electrons. Quantum numbers are simply the address for each electron. Each electron will have 4 quantum numbers. For ease in explaining, I'm going to simplify addresses down to state, street, house, and name.

The principle quantum number (n) indicates which main energy level that electron resides in (state). The angular momentum quantum (l) number indicates the shape of the orbital (street). The magnetic quantum number (m) indicates the orientation of that orbital around the nucleus (house), and the spin quantum number (+1/2 or -!/2) tells which way the electron is moving (name).

Each piece of information is slightly more specific, but any one of them alone basically means nothing. Saying a particular electron is in energy level 3 is akin to saying a particular person lives in Georgia. It's not really useful because a whole lot of people live in the state of Georgia. If I tried to send a letter to that person by simply addressing it by their name and big bold letters saying GEORGIA, it would be returned to me.

So what do all those numbers and letters mean? (My teacher talks too fast!)
principal quantum number (n) - main energy level; can be 1, 2, 3, 4, 5, 6, and so forth but usually doesn't go much past 7

angular momentum quantum number (l) - shape;
s is spherical, these can hold only one orbital containing up to two electrons
p orbitals are lobed shape there can be up to 3 p orbitals in any given main energy level except the first. Therefore, if there are 3 p orbitals that can each hold 2 electrons, there can be a total of 6 electrons held in a p subshell.
d - the d subshell contains 5 orbitals, therefore, d subshells are capable of holding 10 electrons
spin - indicated by +1/2 or -1/2 simply means that the two electrons in any one orbital must be spinning in opposite directions.

For example: 1s2 is the electron configuration for helium's two electrons. Both electrons are in main energy level 1 (principal), in a spherical orbital (angular momentum), [note: there is only one orientation for s orbitals because there is only one to begin with] and one is spinning clockwise and the other counterclockwise.

Did I lose you yet?

There are several kinds of notation, but electron configuration is generally the middle ground one. Noble gas notation is the easiest, so I will probably use that from time to time. Noble gas notation is just like electron configuration, but it is an abbreviated version.

For example: Lithium has the electron configuration 1s2 2s1 and a noble gas notation of [He] 2s1. Now this may not seem like you saved a lot of work but consider sodium's two configurations. 1s2 2s2 2p6 3s1 and [Ne] 3s1. Simply putting Neon in brackets is saying that sodium has the same electron configuration as neon except for the 3s1 which accounts for the 11th electron.

Incidentally, I can't readily do exponents here, but these configurations should have a big number, letter, and superscripted second number. So 1s2 would have a normal 1 followed by s and the 2 would be a superscript. (I'm avoiding carot usage because it's going to get messy really soon.)

If you see a configuration, if you count each number, you should be able to tell which element is being shown. This is because the number of electrons should correspond to the number of protons which is indicated by the atomic number.

Quick cheat sheet: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 should get you up through strontium. Be careful though because there are some funny ones in there, most notably Cr and Cu. What I have shown you is the electron configuration in the order that the orbitals fill, but some textbooks show numerical order. Be sure you know what your particular teacher is asking for.

Why bother? The more you know about quantum numbers, the better a grasp you may have of the elements and how they behave (react).