Constructing the Golden Ratio Using Angle Bisection
Pi (π) and the golden ratio (φ) are the most fascinating constants in mathematics. But unlike π, the golden ratio is a constructible number and since so many people are fascinated with this number, many ingenious methods of constructing this number were devised by various people. In this hub I want to show another method of constructing the golden ratio φ≈1.6180 and the golden ratio conjugate Φ≈0.6180. This method involves bisecting two angles and I show this method because I couldn’t find it anywhere else.
The Bisection Method
We can start with the segment OA=1. Using basic constructions techniques we can make the segment AB=2 perpendicular to OA . Also we can make OC=1 as an extension of OA and CD = 2 , with CD perpendicular to OC . It is also important to make a dotted line that passes though points A and B. Image 1 shows the initial setup. To construct φ and Φ we simply bisect the angles AOD and AOB and mark the intersection points of the bisector lines with the dotted line or segment AB. The line that bisects AOB intersects AB at E and the line that bisects AOD intersects the dotted line at F. We finally have AE=Φ=1⁄ φ and AF=φ. Image 2 shows the actual values of all the angles and segments. In image 2 I also included the fact that the segments OE and OF are perpendicular. Thus to be faster we can construct only the angle AOB , bisect it and then construct the perpendicular to the bisector at point O. Image 3 shows the constructions without the additional segments OC and CD.
Initial Setup
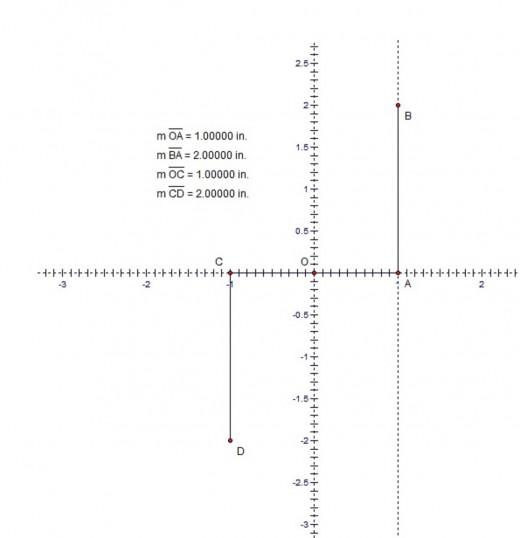
Using Angle Bisection to Construct the Golden Ratio
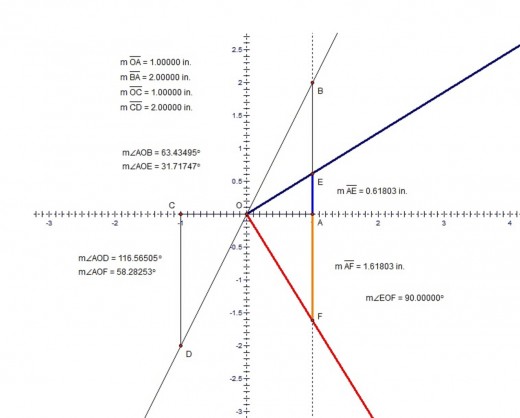
Using Angle Bisection and Perpendicular Line to Construct the Golden Ratio
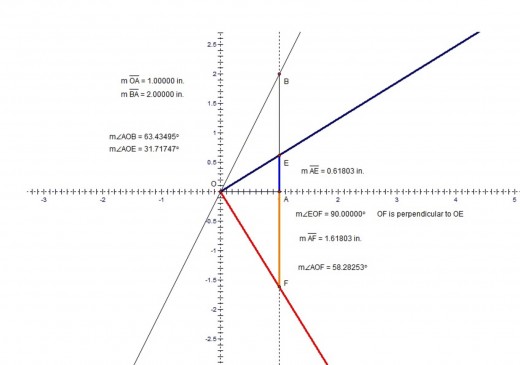
Analysis
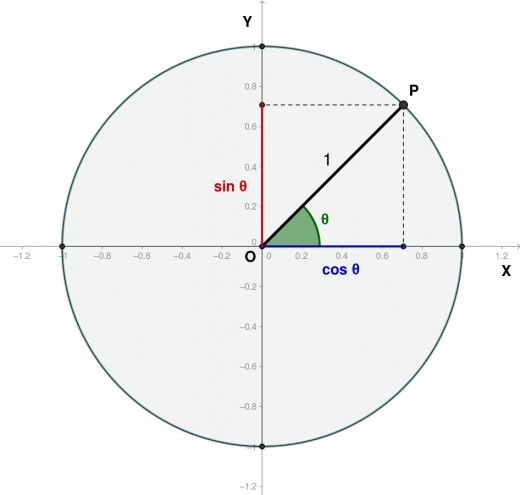
As a reminder we have tan(θ) = Opposite/Adjacent = sin(θ)/cos(θ). Also by looking at Image 4 we see that tan(θ) has a positive value when 0≤θ<90, a negative value when 90<θ≤180 and undefined when θ=90 since cos(90)=0 and we cannot divide by 0. By looking at the graph from Image 2 we see that tan(AOB)=2 and tan(AOD)=-2. We can also see that tan(AOE)=Φ and tan(AOF)=φ. Finally we know that AOB=2AOE and AOD=2AOF.
To check our results we can use the formula for tangent of double angle : tan(2θ)=2tan(θ)/1-tan2(θ). Using the fact that tan(AOE)=Φ and AOB=2AOE by looking at image 5 we see that we get tan(AOB)=2 as expected. In image 5 I also show that the formula gives the expected answer also for tan(AOD)=-2. I should add that in the equations from image 5 I used the fact that Φ=1/φ and φ+1=φ2.